Contrast analysis with R: Tutorial for factorial mixed designs

In this tutorial I will show how contrast estimates can be obtained with R. Previous posts focused on the analyses in factorial between and within designs, now I will focus on a mixed design with one between participants factor and one within participants factor. I will discuss how to obtain an estimate of an interaction contrast using a dataset provided by Haans (2018).

I will illustrate two approaches, the first approach is to use transformed scores in combination with one-sample t-tests, and the other approach uses the univariate mixed model approach. As was explained in the previous tutorial, the first approach tests each contrast against it’s own error variance, whereas in the mixed model approach a common error variance is used (which requires statistical assumptions that will probably not apply in practice; the advantage of the mixed model approach, if its assumptions apply,  is that the Margin of Error of the contrast estimate is somewhat smaller).

Again, our example is taken from Haans (2018; see also this post. It considers the effect of students’ seating distance from the teacher and the educational performance of the students: the closer to the teacher the student is seated, the higher the performance. A “theory “explaining the effect is that the effect is mainly caused by the teacher having decreased levels of eye contact with the students sitting farther to the back in the lecture hall. To test that theory, a experiment was conducted with N = 9 participants in a factorial mixed design (also called a split-plot design), with two fixed factors: the between participants Sunglasses (with or without), and the within participants factor Location (row 1 through row 4). The dependent variable was the score on a 10-item questionnaire about the contents of the lecture. So, we have a 2 by 4  mixed factorial design, with n = 9 participants in each combination of the factor levels.

We will again focus on obtaining an interaction contrast: we will estimate the extent to which the difference between the mean retention score on the first row and those on the other rows differs between the conditions with and without sunglasses.

Using SPSS

Per contrast error variance

Let us first have look at obtaining the estimate with the per contrast error variance approach.

I have used the following SPSS syntax to obtain the estimate of the interaction contrast. I used the SPSS file Mixed2by4data.sav, which is available from the supplementary materials of Haans (2018).

GLM row1 row2 row3 row4 BY sunglasses
 /WSFACTOR=location 4
 /MMATRIX= "First row mean versus mean of the other rows" 
 ALL  1 -1/3 -1/3 -1/3
 /LMATRIX= "Differs between with or without sunglasses?"
 sunglasses 1 -1 intercept 0
 /MEASURE=retention
 /WSDESIGN=location
 /DESIGN=sunglasses.

The result is as follows.

Figure 1: SPSS interaction contrast estimate in a factorial mixed design.

The contrast estimate equals 1.0, 95% CI [ -0.53, 2.53], indicating that the difference between the first row mean and the means of the other rows is estimated to be 1 point larger (on the retention scale) when the teacher does not wear sunglasses compared to when the teacher does wear them.  The width of the confidence interval suggests that this estimate is rather imprecise, which can be expected with such  a small sample. (For more detailed information considering sample size planning for contrastanalysis see: http://small-s.science/?p=10)

Mixed model approach

If you want to use the mixed model approach, you can do the following. (Make sure you have restructured the data into long format; download my version here).

MIXED retention BY sunglasses row
  /FIXED=sunglasses row sunglasses*row | SSTYPE(3)
  /TEST "Interaction" sunglasses*row 1 -1/3 -1/3 -1/3 -1 1/3 1/3 1/3
  /METHOD=REML
  /RANDOM=INTERCEPT | SUBJECT(person) COVTYPE(VC).

Running this syntax will render the following result.

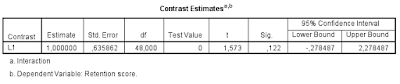Figure 2: SPSS mixed linear model contrast estimate.

The contrast estimate equals 1.0, 95% CI [-0.28, 2.28]. The interpretation is the same as above, of course.

Obtaining the estimates with R

Let’s do the same as above and start with estimating the contrast and the confidence interval with a per-contrast error variance. (For background details with respect to the calculation of the contrastScores, see the post on the analysis of the within-subjects design).

Per contrast error variance

library(foreign)

theData = as.data.frame(read.spss(file="./Mixed2by4data.sav"))


#contrast for within participants factor: 

myContrast = c(1, -1/3, -1/3, -1/3)

contrastScores = as.matrix(theData[,3:6]) %*% myContrast

t.test(contrastScores ~ sunglasses, data=theData)

## 
##  Welch Two Sample t-test
## 
## data:  contrastScores by sunglasses
## t = 1.3846, df = 15.875, p-value = 0.1853
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -0.5320236  2.5320236
## sample estimates:
## mean in group Without glasses    mean in group With glasses 
##                      2.666667                      1.666667

#assuming equal variances: 

t.test(contrastScores ~ sunglasses, var.equal=TRUE, data=theData)

## 
##  Two Sample t-test
## 
## data:  contrastScores by sunglasses
## t = 1.3846, df = 16, p-value = 0.1852
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -0.5310427  2.5310427
## sample estimates:
## mean in group Without glasses    mean in group With glasses 
##                      2.666667                      1.666667

library(lme4) # not necesary if you want to use aov
library(emmeans)

# set options for emmeans to get both p-value and ci
emm_options(contrast = list(infer=c(TRUE, TRUE)))
theData = as.data.frame(read.spss(file="./Mixed2by4dataLong.sav"))
theData$person = factor(theData$person)

attach(theData)

myContrast = c(1, -1/3, -1/3, -1/3, -1, 1/3, 1/3, 1/3)

# using the lmer model 

myMod.lme = lmer(retention ~ sunglasses*location + (1|person))

# note: in the model formula I used between * within (i.e. 
# sunglasses * location). In the call to emmeans below, I have used
# the reverse notation: location*sunglasses. This has to do with
# the way I formulated the contrast: the first 4 weights are for
# the condition without sunglasses and the last 4 weights are for
# the condition with sunglasses. So, the weights are (so to say)
# specified as a 4 x 2 design, and the model as a 2 x 4 design (which
# is more or less the traditional way of specifying the anova model:
# first the between factor(s) than the within factor(s) followed by
# all the interactions).

condMeans = emmeans(myMod.lme, ~location*sunglasses)
contrast(condMeans, list("interaction"= myContrast))

##  contrast    estimate        SE df  lower.CL upper.CL t.ratio p.value
##  interaction        1 0.6358624 48 -0.278487 2.278487   1.573  0.1224
## 
## Confidence level used: 0.95

# using the aov model: 

myMod.aov = aov(retention ~ sunglasses*location + Error(person/location))

condMeans = emmeans(myMod.aov, ~location*sunglasses)

contrast(condMeans, list("interaction"= myContrast))

##  contrast    estimate        SE df  lower.CL upper.CL t.ratio p.value
##  interaction        1 0.6358624 48 -0.278487 2.278487   1.573  0.1224
## 
## Confidence level used: 0.95

Reference
Haans, Antal (2018). Contrast Analysis: A Tutorial. Practical Assessment, Research, & Education, 23(9). Available online: http://pareonline.net/getvn.asp?v=23&n=9