Methodology Archives - The small S scientist

March 2, 2021May 1, 2021

Comparing the quantiles of two groups

Comparing the quantiles of two groups provides information that is lost by simply looking at means or medians. This post shows how to do that.

Traditionally, the comparison of two groups focuses on comparing means or medians. But, as Wilcox (2012) explains, there are many more features of the distributions of two groups that we may compare in order to shed light on how the groups differ. An interesting approach is to estimate the difference between the quantiles of the two groups. Wilcox (2012, pp. 138-150) shows us an approach that is based on the shift function. The procedure boils down to estimating the quantiles of both groups, and plotting the quantiles of the first group against the difference between the quantiles.

In order to aid in comparing the quantiles of the groups, I’ve created a function for R that can be used for plotting the comparison between the two groups. The functions uses the ggplot2 package and the WRS package (that can be found here: WRS: A package of R.R. Wilcox’ robust statistics functions version 0.24 from R-Forge (rdrr.io)) ; see also: Installation of WRS package (Wilcox’ Robust Statistics) | R-bloggers (r-bloggers.com).).

library(WRS)
library(ggplot2)

plotSband <- function(x, y, x.name = "Control") {
  x <- sort(x[!is.na(x)])
  y <- sort(y[!is.na(y)]) 
  qhat <- 1:length(x)/length(x)
  idx.y <- floor(qhat*length(y) + .5)
  idx.y[idx.y <= 0] <- 1
  idx.y[idx.y > length(y)] <- length(y)
  
  delta <- y[idx.y] - x
  
  cis <- WRS::sband(x, y, plotit=F)$m[, c(2, 3)]
  
  check.missing <- apply(cis, 2, function(x) sum(is.na(x)))
  if (sum(check.missing == length(x)) > 1) {
    stop("All CI limits equal to - or + Infinity")
  }
  ylims <- c(min(cis[!is.na(cis[,1]), 1]) - .50, 
             max(cis[!is.na(cis[,2]), 2]) + .50)
  
  cis[is.na(cis[, 1]), 1] <- ylims[1]*5
  cis[is.na(cis[, 2]), 2] <- ylims[2]*5
  
  thePlot <- ggplot(mapping = aes(x)) + 
    xlab(x.name) + 
    geom_smooth(aes(x = x, y = delta), se = F, col="blue") + 
    ylab("Delta") +
    geom_point(aes(x = quantile(x, c(.25, .50, .75)), 
                   y = rep(ylims[1], 3)), pch=c(3, 2, 3), size=2) +
    geom_ribbon(aes(ymin = cis[,1], ymax = cis[,2]), alpha=.20) + 
    coord_cartesian(ylim = ylims)
  suppressMessages(print(thePlot))
}

Let’s look at an example. Figure 1 presents data from an experiment investigating the persuasive effect of narratives on intentions of adopting a healthy lifestyle (see for details Boeijinga, Hoeken, and Sanders (2017)). The plotted data are the differences in intention between the quantiles of a group of participants who read a narrative focusing on risk-perception (detailing the risks of unhealthy behavior) and a group of participants who read a narrative focusing on action-planning (here called the control group), focusing on how the healthy behavior may actually be implemented by the participant.

Comparing the quantiles of two groups — Figure 1. Output from the plotSband-function

Figure 1 shows the following. The triangle is the median of the data in the control group, and the plusses the .25th and .75th quantiles. The shaded regions define the simultaneous 95% confidence intervals for the differences between the quantiles of the two groups. Here, these regions appear quite ragged, because of the discrete nature of the data. For values below 2.5 and above 3.5, the limits (respectively the lower and upper limits of the 95% CI’S) equal infinity, so these values extend beyond the limits of the y-axis. (The sband function returns NA for these limits). The smoothed-regression line should help interpret the general trend.

How can we interpret Figure 1? First of all, if you think that it is important to look at statistical significance, note that none of the 95% intervals exclude zero, so none of the differences reach the traditional significance at the .05 level. As we can see, none of them exclude differences as large as -0.50 as well, so we should not be tempted to conclude that because zero is in the interval that we should adopt zero as the point-estimate. For instance, if we look at x = 2.5, we see that the 95% CI equlas [-1.5, 0.0], the value zero is included interval, but so is the value -1.5. It would be unlogical to conclude that zero is our best estimate if so many values are included in the interval.

The loess-regression line suggests that the differences in quantiles between the two groups of the narrative is relatively steady for the lower quantiles of the distribution (up to the x = 3.0, or so; or at least below the median), but for quantiles larger than the median the effect gets smaller and smaller until the regression line crosses zero at the value x = 3.75. This value is approximately the .88 quantile of the distribution of the scores in the control condition (this is not shown in the graph).

The values on the y-axis are the differences between the quantiles. A negative delta means that the quantile of the control condition has a larger value than the corresponding quantile in the experimental condition. The results therefore suggest that participants in the control condition with a relatively low intention score, would have scored even lower in the other condition. To give some perspective: expressed in the number of standard deviations of the intention scores in the control group a delta of -0.50 corresponds to a 0.8 SD difference.

Note however, that due to the limited number of observations in the experiment, the uncertainty about the direction of the effect is very large, especially in the tails of the distribution (roughly below the .25 and above the .75 quantile). So, even though the data suggest that Action Planning leads to more positive intentions, especially for the lower quantiles, but still considerably for the .75 quantile, a (much) larger dataset is needed to obtain more convincing evidence for this pattern.

December 10, 2020April 18, 2022

Cohen’s d for paired designs

For the paired design, which is traditionally used to obtain data for the paired t-test, we can calculate a standardized mean difference, Cohen’s d, using the average of the standard deviations of the two conditions. Cohen’s d for paired designs can be calculated as follows.

d_{av} =\frac{(M_1 - M_2)}{s_{av}}, \tag{1}

where $s_{av}$ equals

s_{av}= \sqrt{\frac{1}{2}(S^2_1+S^2_2)}. \tag{2}

Now, (1) is of course an estimate of (3), the population value of Cohen’s d for paired designs, but we do not only need a point estimate, but also a confidence interval.

The following R-code can be used to obtain a 95% confidence interval for the estimate of $\delta_{av}$ , the population mean difference standardized by using the average of the two standard deviations:

\delta_{av} = \frac{\mu_1 - \mu_2}{\sqrt{\frac{1}{2}(\sigma_1^2 + \sigma_2^2)}} , \tag{3}

This procedure uses the approximate procedure by Algina & Keselman (2003), which is also used by ESCI (Cumming, 2012; Cumming and Calin-Jageman, 2017), as Kline (2013) explains. The following steps are performed to obtain the 95% confidence interval.

Use the obtained t-value of the paired t-test to estimate the non-centrality parameter $\lambda$ . Steps 2 and 3 are for calculating a 95% confidence interval for the non-centrality parameter.
Use an iterative procedure to find the non-centrality parameter of the t-distribution for which the observed t-value is the .025 quantile. This is the upper limit of the confidence interval for the non-centrality parameter.
Use an iterative procedure to find the non-centrality parameter of the t-distribution for which the observed t-value is the .975 quantile. This is the lower limit of the confidence interval for the non-centrality parameter.
To obtain a CI for $\delta_{av}$ multiply the limits of the confidence interval for the non-centrality parameter by the value $\sqrt{\frac{2S_D^2}{n(S_1^2+S_2^2)}}$ where n is the sample size, $S_D^2$ the variance of the difference scores , and $S_1^2$ and $S_2^2$ the variances of the two variables.

The following R-function does all the work. Note that with large potential values for the noncentrality parameter R issues warnings that “full precision has not been achieved in ‘pnt{final}'”. These warnings can be ignored ( I checked many examples against ESCI’s output), but in order to prevent them, I let the optimize function search from the observed value of t to maximally five times its value, and I have included the option to suppress warnings or not (just set warn = TRUE to get the warnings).

ci.d.av <- function(t, n, s.1, s.2, s.diff, warn = FALSE) {
  if (t < 1) {
    lims <- c(-5, 5)
  } else {
    lims <- c(-5*abs(t), 5*abs(t))
  }
  df = n - 1
  multiplier = sqrt((2*s.diff^2) / (n*(s.1^2 +  s.2^2)) )
  loss <- function(x, prob) (pt(t, df, x) - prob)^2  
  if (warn == FALSE) {
    ul <- suppressWarnings(optimize(loss, lims, prob=.025))$minimum 
    ll <- suppressWarnings(optimize(loss, lims, prob=.975))$minimum
  } else {
    ul <- optimize(loss, lims, prob=.025)$minimum 
    ll <- optimize(loss, lims, prob=.975)$minimum
  } 
    return(round(c(ll, ul), 4)*multiplier)  
}

The arguments of the function are t, the t-value of the t-test testing the hypothesis of equal population means, the sample size (n), the standard deviations (s.1 and s.2) of the two variables and the standard deviation of the difference scores (s.diff).

Calculating Cohen’s d for paired designs: an example

Here is a quick example.

library(MASS)
set.seed(1234)

# generate random multivariate normal data with sample size n = 20

theData <- mvrnorm(20, c(.5, .0), matrix(c(1, .8, .8, 1), 2, 2))

# calculate the standard deviations 

sds <- apply(theData, 2, sd)

# calculate the standard deviation of difference scores 

sDiff <- sd(theData[,1] - theData[,2])

# get t.value and a value for d.av 
# here I use the output of the t-test in R to obtain t and the mean
# difference score (needed for calculating d.av)

theTest <- t.test(theData[,1], theData[,2], paired=TRUE)
t = theTest$statistic
d.av = theTest$estimate / mean(sds)

ci.d.av(t = t, n = 20, s.1 = sds[1], s.2 = sds[2], sDiff)

The results are that the estimate equals $d_{av} = 0.87, 95\% \text{CI} [0.51, 1.22].$

Alternatively, we can make use of the conf.limits.nct function of the MBESS package (Kelley, 2007a, 2007b), and proceed as follows (using the data generated above).

library(MBESS)

ci.d.av.2 <- function(t, n, s.1, s.2, s.diff) {
  df = n - 1
  multiplier = sqrt((2*s.diff^2) / (n*(s.1^2 +  s.2^2)) )
  unlist(conf.limits.nct(t, df)[c(1,3)])*multiplier
}

ci.d.av.2(t = t, n = 20, s.1 = sds[1], s.2 = sds[2], s.diff = sDiff).

References

Algina, J. & Keselman, H. J. (2003). Approximate confidence intervals for effect sizes. Educational and Psychological Measurement, 63, 721-734.

Cumming, G. (2012). Understanding the New Statistics. Effect Sizes, Confidence Interval, and Meta-Analysis. New York: Routledge.

Cumming, G. & Calin-Jageman, R. (2017). Introduction fo the New Statistics. Estimation, Open Science, and Beyond. New York: Routledge.

Kelley, K. (2007b). Confidence intervals for standardized effect sizes: Theory, application, and implementation. Journal of Statistical Software, 20(8), 1-24.

Kelley, K. (2007a). Methods for the Behavioral, Educational, and Social Sciences: An R Package. Behavior Research Methods, 39, 979–984.

Kline, R.b. (2013). Beyond Significance Testing. Statistics Reform in the Behavioral Sciences. (Second Edition). Washington: APA.

March 26, 2019October 22, 2019

The Anatidae Principle

If it looks like a duck, and quacks like a duck, we have at least to consider the possibility that we have a small aquatic bird of the family Anatidae on our hands.
– Douglas Adams

I like to teach my students how they can apply to their data-analysis what I call the Anatidae Principle (or the Principle of the Duck). (The name is obviously inspired by the above quote from Douglas Adam’s Dirk Gently’s Holistic Detective Agency).

For the purpose of data-analysis, the Anatidae Principle simply boils down to the following: If it looks like you found a relation, difference, or effect in your sample you should at least consider the possibility that there indeed is a relation, difference or effect. That is, look at your data, summarize, make figures, and think (hard) about what your data potentially mean for the answer to your research question, hypotheses, hunches, whatever you like. Do this before you start calculating p-values, confidence intervals, Bayes Factors, Posterior distributions, etc., etc.

In my experience, researchers too often violate the Anatidae Principle: they calculate a p-value, and if it is not significant they simply ignore their sample results. Never mind that, as they predicted, group A outperforms group B, if it is not significant, they will claim they found no effect. And, worse still, believe it.

Kline (2013) ) (p. 117) gives solid advice:

“Null hypothesis rejections do not imply substantive significance, so researchers need other frames of reference to explain to their audiences why the results are interesting or important. A start is to learn to describe your results without mention of statistical significance at all. In its place, refer to descriptive statistics and effect sizes and explain why those effect sizes matter in a particular context. Doing so may seem odd at first, but you should understand that statistical tests are not generally necessary to detect meaningful or noteworthy effects, which should be obvious to visual inspection of relatively simple kinds of graphical displays (Cohen, 1994). The description of results at a level closer to the data may also help researchers to develop better communication skills.”

March 22, 2019October 22, 2019

Planning with assurance, with assurance

Planning for precision requires that we choose a target Margin of Error (MoE; see this post for an introduction to the basic concepts) and a value for assurance, the probability that MoE will not exceed our target MoE. What your exact target MoE will be depends on your research goals, of course.

Cumming and Calin-Jageman (2017, p. 277) propose a strategy for determining target MoE. You can use this strategy if your research goal is to provide strong evidence that the effect size is non-zero. The strategy is to divide the expected value of the difference by two, and to use that result as your target MoE.

Let’s restrict our attention to the comparison of two means. If the expected difference between the two means is Cohens’s d = .80, the proposed strategy is to set your target MoE at f = .40, which means that your target MoE is set at .40 standard deviations. If you plan for this value of target MoE with 80% assurance, the recommended sample size is n = 55 participants per group. These results are guaranteed to be true, if it is known for a fact that Cohen’s d is .80 and all statistical assumptions apply.

But it is generally not known for a fact that Cohen’s d has a particular value and so we need to answer a non-trivial question: what effect size can we reasonably expect? And, how can we have assurance that the MoE will not exceed half the unknown true effect size? One of the many options we have for answering this question is to conduct a pilot study, estimate the plausible values of the effect size and use these values for sample size planning. I will describe a strategy that basically mirrors the sample size planning for power approach described by Anderson, Kelley, and Maxwell (2017).

The procedure is as follows. In order to plan with approximately 80% assurance, estimate on the basis of your pilot the 80% confidence interval for the population effect size and use half the value of the lower limit for sample size planning with 90% assurance. This will give you 81% assurance that assurance MoE is no larger than half the unknown true effect size.

The logic of planning with assurance, with assurance

There are two “problems” we need to consider when estimating the true effect size. The first problem is that there is at least 50% probability of obtaining an overestimate of the true effect size. If that happens, and we take the point estimate of the effect size as input for sample size planning, what we “believe” to be a sample size sufficient for 80% assurance will be a sample size that has less than 80% assurance at least 50% of the times. So, using the point estimate gives assurance MoE for the unknown effect size with less than 50% assurance.

To make it more concrete: suppose the true effect equals .80, and we use n = 25 participants in both groups of the pilot study, the probability is approximately 50% that the point estimate is above .80. This implies, of course, that we will plan for a value of f > .40, approximately 50% of the times, and so the sample we get will only give us 80% assurance 50% of the times.

The second problem is that the small sample sizes we normally use for pilot studies may give highly imprecise estimates. For instance, with n = 25 participants per group, the expected MoE is f = 0.5687. So, even if we accept 50% assurance, it is highly likely that the point estimate is rather imprecise.

Since we are considering a pilot study, one of the obvious solutions, increasing the sample size so that expected MoE is likely to be small, is not really an option. But what we can do is to use an estimate that is unlikely to be an overestimate of the true effect size. In particular, we can use as our estimate the lower limit of a confidence interval for the effect size.

Let me explain, by considering the 80% CI of the effect size estimate. From basic theory it follows that the “true” value of the effect size will be smaller than the lower limit of the 80% confidence interval with probability equal to 10%. That is, if we calculate a huge number of 80% confidence intervals, each time on the basis of new random samples from the population, the true value of the effect size will be below the lower limit in 10% of the cases. This also means that the lower limit of the interval has 90% probability to not overestimate the true effect size.

This means that if we take the lower limit of the 80% CI of the pilot estimate as input for our sample size calculations, and if we plan with assurance of .90, we will have 90%*90% = 81% assurance that using the sample size we get from our calculations will have MoE no larger than half the true effect size. (Note that for 80% CI’s with negative limits you should choose the upper limit).

Sample Size planning based on a pilot study

Student of mine recently did a pilot study. This was a pilot for an experiment investigating the size of the effect of fluency of delivery of a spoken message in a video on Comprehensibility, Persuasiveness and viewers’ Appreciation of the video. The pilot study used two groups of size n = 10, one group watched the fluent video (without ‘eh’) and the other group watched the disfluent video where the speaker used ‘eh’ a lot. The dependent variables were measured on 7-point scales.

Let’s look at the results for the Appreciation variable. The (biased) estimate of Cohen’s d (based on the pooled standard deviation) equals 1.09, 80% CI [0.46, 1.69] (I’ve calculated this using the ci.smd function from the MBESS-package. According to the rules-of-thumb for interpreting Cohen’s d, this can be considered a large effect. (For communication effect studies it can be considered an insanely large effect). However, the CI shows the large imprecision of the result, which is of course what we can expect with sample sizes of n = 10. (Average MoE equals f = 0.95, and according to my rules-of-thumb that is well below what I consider to be borderline precise).

If we use the lower limit of the interval (d = 0.46), sample size planning with 90% assurance for half that effect (f = 0.23) gives us a sample size equal to n = 162. (Technical note: I planned for the half-width of the standardized CI of the unstandardized effect size, not for the CI of the standardized effect size; I used my Shiny App for planning assuming an independent groups design with two groups). As explained, since we used the lower limit of the 80% CI of the pilot and used 90% assurance in planning the sample size, the assurance that MoE will not exceed half the unknown true effect size equals 81%.

October 14, 2017March 27, 2021

The omnibus F-test may be ignored if you use multiple comparison procedures

I think trying to be scientific with a small s involves asking critical questions about common wisdom or common practice. In this post, I would like to focus on multiple comparisons in the context of ANOVA. What does common practice indicate?

Common wisdom suggests doing multiple comparisons only if the F-test is significant

Let’s have a look on some practical advice considering multiple comparisons found on the web (R-bloggers.com) and in Field (2015).

“One way to begin an ANOVA is to run a general omnibus test. The advantage to starting here is that if the omnibus test comes up insignificant, you can stop your analysis and deem all pairwise comparisons insignificant. If the omnibus test is significant, you should continue with pairwise comparisons” (https://www.r-bloggers.com/r-tutorial-series-one-way-anova-with-pairwise-comparisons/)

“When we have a statistically significant effect in ANOVA and an independent variable of more than two levels, we typically want to make follow-up comparisons. There are numerous methods for making pairwise comparisons and this tutorial will demonstrate how to execute several different techniques in R.” (https://www.r-bloggers.com/r-tutorial-series-anova-pairwise-comparison-methods/)
And have a look at how the text book I used to use in my statistics course explains it.

“It might seem a bit unhelpful that an ANOVA doesn’t tell you which groups are different from which, given that having gone to the trouble of running an experiment, you probably need to know more than ‘there’s some difference somewhere or other’. You might wonder, therefore, why we don’t just carry out a lot of t-tests, which would tell us very specifically whether pairs of group means differ. Actually, the reason has already been explained in Section 2.1.6.7: every time you run multiple tests on the same data you inflate the potential Type I errors that you make. However, we’ll return to this point in Section 11.5 when we look at how we follow up an ANOVA to discover where the group difference lie.” (Field, 2015, p. 442).
Although, in honesty, on p. 459 Field writes:

“The least significance difference (LSD) pairwise comparison makes no attempt to control Type I error and is equivalent to performing multiple t-tests on the data. The only difference is that LSD requires the overall ANOVA to be significant.”

This is meant to inform about the relative merits of one post hoc procedure to another in terms of Type I and Type II error. Crucially, it is not mentioned that the other post-hoc procedures require that the overall ANOVA be significant. (As common wisdom seems to suggest). However, his flow-chart of the ANOVA procedure (p. 460) clearly suggests multiple comparison procedures should be used as post-hoc procedures (after the ANOVA is significant).

Thus, common “statistical” wisdom seem to suggest that multiple comparison procedures are to be used as post hoc procedures following up a significant omnibus F-test. And the reason is that this two-stepped procedure minimizes the probability of type I errors.

Now, let’s ask ourselves whether this common sense is, well, sensible.

Multiple comparisons only after significant F-test affects power negatively

Wilcox (2017) contains some useful information regarding our question. In his discussion of the much used Tukey-HSD procedure (the Tukey-Kramer Method), he references Bernhardson, (1975) who shows that the probability of at least 1 type I error among pairwise comparisons of estimates of equal population means (i.e. true null-hypotheses) is no longer equal to $\alpha$ if the procedure is only carried out following a significant omnibus test. That is, if we use our beloved two step procedure.

The consequence of the two step procedure for the Tukey-HSD is that $\alpha$ is reduced. Thus, if we want our multiple comparisons procedure to generate one type I error or more at most with a probability of $\alpha = .05$ , using the 2 step procedure leads to a lowered $\alpha$ . This is of course, bad news, because in the event that not all of the null-hypotheses are true, lowering $\alpha$ increases $\beta$ , the probability of not rejecting when the null-hypothesis is false (keeping the sample size constant, of course). In other words, the two step procedure decreases the power of the multiple comparison procedure.

In the words of Wilcox (2017):

“In practical terms, when it comes to controlling the probability of at least one type I error, there is no need to first reject with the ANOVA F test to justify using the Tukey-Kramer method. If the Tukey-Kramer method is used only after the F test rejects, power can be reduced. Currently, however, common practice is to use the Tukey-Kramer method only if the F-test rejects. That is, the insight reported by Bernhardson is not yet well known.” (p. 385).

In conceptual terms, the fact that the probability of at least one type I error in the multiple comparison procedure is smaller than $\alpha$ if the F-test rejects is pretty clear, at least to me it is. Suppose we reject if the p-value of the F-test is smaller or equal to 5%. This will also be the probability that we conduct the multiple comparison test over repeated replications of the same experiment. Of that 5%, not every application of the procedure will result in at least one type I error. Indeed, a puzzling fact for many beginning researchers is that the F-test is significant while none of the pairwise comparisons is. In other words, some of those 5% of the cases in which we perform the procedure following a significant F-test will probably not reject any of the pairwise null-hypotheses, unless it is guaranteed that at least one type I error per application will be made.

(With no adjustment of $\alpha$ for multiple comparisons, this will happen (with high probability so no guarantee) if a huge number of pairwise comparisons are made. For instance, with 99 unadjusted multiple comparisons the probability of at least one type I error is 99%.; this is why it makes sense to demand that the F-test is significant before testing multiple comparisons with the LSD procedure. Although the latter seems to run into trouble with more than 3 groups (Wilcox, 2017).

A quick simulation study

My hunch is that the two-step procedure is unnecessary for the Tukey-Kramer method as well as for other multiple comparison procedures (the exception Fisher’s LSD procedure which was designed as a post hoc procedure to be used as a follow up after a significant F-test, as Field (2015) rightly points out), but I only focused on the Tukey-Kramer method. What I did was a simple simulation study with a four group between subjects design (all $\mu$ ‘s equal) and estimated the probability of at least type I error both with and without using the 2 step procedure.

set.seed(456)
#number of groups
ngr = 4

#number of participants
n = 40

#group is a factor
gr <- factor(rep(1:ngr, each=n))

#vector for storing rejections F-test
Reject <- rep(0, 10000)

#vector for storing #rejections multiple
#comparisons
RejectHSD <- rep(0, 10000)

for (i in 1:10000) {

y = rnorm(ngr*n)
mod = aov(y ~ gr)
Reject[i] = anova(mod)$"Pr(>F)"[1] <= .05
PS <- TukeyHSD(mod)$gr[,4]
RejectHSD[i] = sum(PS <=.05)
}

#probability type I error F-test
sum(Reject)/length(Reject)

## [1] 0.0515

#probability at least one type I error Tukey HSD
sum(RejectHSD > 0) / length(RejectHSD)

## [1] 0.0503

#probability at least one type I error given F-tests Rejects
sum(RejectHSD[Reject==TRUE] > 0) / length(RejectHSD)

## [1] 0.0424

Even though a single (relatively tiny) simulation (which, by the way, takes a long time to run, nonetheless), is not necessarily convincing, it does illustrate the main points of this post. First, the probability of at least one incorrect rejection using the TukeyHSD function is close to .05. With this particular random seed it even performs a little better than the ANOVA F-test: .0503 versus .0515. This illustrates that even without considering whether the omnibus test is significant the main demand of not rejecting too many true null-hypotheses is completely satisfied. So, in practical terms, you can safely ignore the omnibus test if your concerns are about $\alpha$ .

Second, the probability of incorrectly rejecting at least one true pair-wise null-hypothesis after the ANOVA F-test is significant is estimated to be .0424. This shows, that the two-step procedure leads to a larger decrease in the actual type I error probability than is wanted. Even though this may seem good news from the perspective of avoiding type I errors, the down side is that pair wise null-hypotheses that are false (and potentially important) may not be detected.

Conclusion

Common wisdom and practice suggest that multiple comparisons procedures should be done only after a significant omnibus test. We have seen that this is not at all necessary if we use a multiple comparisons procedure that is designed to control the type I error probability. To my knowledge, most of the procedures conventionally thought of as post hoc tests are designed in this manner, the exception being the LSD procedure which does require a significant F-test. For practical purposes, then, do not bother with the omnibus test (note the exception) if you are planning to pair wise compare all the treatment means.

This practical advice does not mean, of course, that I am suggesting you spend your time comparing all treatment means. Most of the time, focused comparisons are a more fruitful way of analysing your data. But I’ll leave that topic for another time.

References

Field, A. (2013). Discovering Statistics Using IBM SPSS Statistics. 4th Edition. London: Sage.

Wilcox, R. (2017). Understanding and Applying Basic Statistical Methods Using R. Hoboken, NJ: Wiley,

July 25, 2017November 7, 2019

Planning for a precise interaction contrast estimate

In my previous post (here), I wrote about obtaining a confidence interval for the estimate of an interaction contrast. I demonstrated, for a simple two-way independent factorial design, how to obtain a confidence interval by making use of the information in an ANOVA source table and estimates of the marginal means and how a custom contrast estimate can be obtained with SPSS.

One of the results of the analysis in the previous post was that the 95% confidence interval for the interaction was very wide. The estimate was .77, 95% CI [0.04, 1.49]. Suppose that it is theoretically or practically important to know the value of the contrast to a more precise degree. (I.e. some researchers will be content that the CI allows for a directional qualitative interpretation: there seems to exist a positive interaction effect, but others, more interested in the quantitative questions may not be so easily satisfied). Let’s see how we can plan the research to obtain a more precise estimate. In other words, let’s plan for precision.

Of course, there are several ways in which the precision of the estimate can be increased. For instance, by using measurement procedures that are designed to obtain reliable data, we could change the experimental design, for example switching to a repeated measures (crossed) design, and/or increase the number of observations. An example of the latter would be to increase the number of participants and/or the number of observations per participant. We will only consider the option of increasing the number of participants, and keep the independent factorial design, although in reality we would of course also strive for a measurement instrument that generally gives us highly reliable data. (By the way, it is possible to use my Precision application to investigate the effects of changing the experimental design on the expected precision of contrast estimates in studies with 1 fixed factor and 2 random factors).

The plan for the rest of this post is as follows. We will focus on getting a short confidence interval for our interaction estimate, and we will do that by considering the half-width of the interval, the Margin of Error (MOE). First we will try to find a sample size that gives us an expected MOE (in repeated replication of the experiment with new random samples) no more than a target MOE. Second, we will try to find a sample size that gives a MOE smaller than or equal to our target MOE in a specifiable percentage (say, 80% or 90%) of replication experiments. The latter approach is called planning with assurance.

Let us get back to some of the SPSS output we considered in the previous post to get the ingredients we need for sample size planning. First, the ANOVA table.

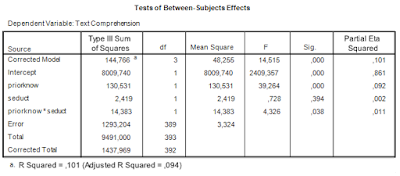Table 1. ANOVA source table

We are interested in estimating and optimizing the precision of an interaction contrast estimate. The first things we need are an expression of the error variance needed to calculate the standard error of the estimate and the degrees of freedom that were used in estimating the error variance. In general, the error variance needed is the same error variance you would use in performing an F-test for the specific effect, in this case the interaction effect.

Thus, we note the error variance used to test the interaction effect, i.e. mean square error, and the degrees of freedom. The value of mean square error is 3.324, and the degrees of freedom are 389. Note that this value is the total sample sizes minus the number of conditions (393 – 4 = 389), or, equivalently, the total sample sizes minus the degrees of freedom of the intercept, the main effects, and the interaction (393 – (1 + 1 + 1 + 1) = 389). I will call these degrees of freedom the error degrees of freedom, df_e.

MOE can be obtained by multiplying a critical t-value with the same degrees of freedom as the error degrees of freedom with the standard error of the estimate.

The standard error of the contrast estimate is

$\hat{\sigma_\psi}= \sqrt{\sum{c_i^2MS_e/n_i}},$

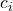where $c_i$ is the contrast weight for the i-th condition mean, and 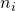$n_i$ the number of observations (in our example participants) in treatment condition i. Note that 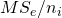$MS_e / n_i$ is the variance of treatment mean i, the square root of which gives the familiar standard error of the mean.

The contrast weights we used to estimate the 2 x 2 interaction were {-1, 1, 1, -1}. So, the expression for MOE becomes

$MOE = t_{.975}(df_e)\sqrt{\sum{c_i^2MS_e/n_i}}=t_{.975}(df_e)\sqrt{4MS_e/n_i} = 2t_{.975}(df_e)\sqrt{MS_e/n_i}.$

Thus, suppose we have the independent 2×2 factorial design, 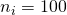$n_i = 100$ , and the true value of Mean Square Error is 3.324, then MOE for the contrast estimate equals

$MOE = 2*t_{.975}(396)*\sqrt{3.324/100} = 0.7071$

.
Note that this is the value of MOE we obtain on average in repeated replications with new samples, if we use sample sizes of 100 (total number of participants is 400) and if the true value of the error variance is 3.324. The value is close to the value we obtained in the previous post (MOE = 0.72) because the sample sizes were very close to 100 per group.

Now, we found the original confidence interval too wide, and we have just seen how 100 participants per group does not really help. MOE is only slightly smaller than our originally obtained MOE. We need to set a target MOE and then figure out how many participants we need to get that target MOE.

Intermezzo: Rules of thumb for target MOE

(Here are some updated rules of thumb: https://the-small-s-scientist.blogspot.com/2018/11/contrast-tutorial.html)

In the absence of theoretical or practical considerations about the precision we want, we may want to use rules of thumb. My (very first proposal for) rules of thumb are based on the default interpretations of Cohen’s d. Considering the absolute values of d ≤ .10 to be negligible d = .20 small, d = .50 medium and d = .80 large. (I really do not like rules-of-thumb, because using them is a sign that you are not thinking).

Now, suppose that we interpret the confidence interval as a range of plausible values for the true value of the effect size. It is not at all clear to me what such a supposition entails, but let’s simply take it for granted right now (please don’t). Then, I think it is reasonable to say that being able to distinguish between small and negligible effects sizes is relatively precise. Thus a MOE of .05 (pooled) standard deviations can be considered precise because (on average) the 95% CI for the small effect sizes is [.15, .25], assuming we know the value of the standard deviation, so negligible effects will not be deemed plausible values on average, since effect sizes smaller than .10 are outside the interval.

By essentially the same reasoning. if we cannot distinguish between large and negligible effects, we are not estimating things very precisely. Therefore, a MOE of .80 standard deviations can be considered to be not very precise. On average, the CI for an existing large effect, will be [0, 1.60], so it includes both negligible and very large effects as plausible values.

For medium (does it make sense to speak of medium precision?) precision I would like to suggest .20-.25 standard deviations. On average, with this value for MOE, if there is a medium effect, small effects and large effects are relatively implausible. In the case of small effects, medium precision entails that on average both effects in the opposite direction and medium effects are among the plausible values.

Of course, I am interpreting the d-values as strict boundaries, but the scale is not categorical, but continuous. So instead of small, large effect sizes, it’s better to speak of smallish and largish effect sizes. And as soon as I find a variant for medium effects sizes I will also include that term in the list.

Note: sample size planning may indicate that precision of MOE = .20-.25 standard deviations is unattainable. In that case, we will simply have to accept that our precision does not lead to confident conclusions about the population effect size. (Once I showed one of my colleagues my precision app, during which he said: “that amount of precision requires a very large sample. I do not like your ideas about sample size planning”).

(By the way, I am also considering rules-of-thumb for target MOE that include assurance. Something like: high precision is when repeated experiments have a high probability of distinguishing small and negligible effects; in that case the average MOE will be smaller than .05).

Planning for precision

Let’s plan for a precision of 0.25 standard deviation. In our case, that standard deviation is the pooled standard deviation: the square root of Mean Square Error. The (estimated) value of Mean Square Error is 3.324 (see Table 1), so our value for the standard deviation is 1.8232. Our target MOE is, therefore, 0.4558.

Let’s make things very clear. Here we are planning for a target MOE based on an estimate of the pooled standard deviation (and on assumptions about the population distribution). In order for our planning to be of practical value, we need some reassurance that that estimate is trustworthy. One way of doing that is to consider the CI for the standard deviation. I will not discuss that topic, and simply give you a CI: [2.90, 3.86].

Take a look at the expression for MOE.

$MOE = 2*t_{.975}(df_e)\sqrt{(MS_w / n_i)},$

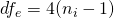where $df_e = 4(n_i - 1)$ , since we are considering the 2×2 design.

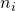
Since our target MOE equals .4588, our goal becomes to solve the following equation for $n_i$ , since we want the sample size:

$0.4558 = 2*t_{.975}(4(n_i - 1)\sqrt{(MS_w / n_i)},$

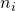
However, because $n_i$ determines both the standard error and the degrees of freedom (and thereby the critical value of t), the equation may be a little hard to solve. So, I will create a function in R that enables me to quite easily get the required sample size. (It is relatively easy to create a more general function (see the Precision App), but here I will give an example tailored to the specific situation at hand).

First we create a function to calculate MOE:

MOE = function(n) {
  MOE = 2*qt(.975, 4*(n - 1))*sqrt(3.324/n)
}

Next, we will define a loss function and use R’s built-in optimize function to determine the sample size. Note that the loss-function calculates the squared difference between MOE based on a sample size n and our target MOE. The optimize function minimizes that squared difference in terms of sample size n (starting with n = 100 and stopping at n = 1000).

loss <- function(n) {
  (MOE(n) - 0.4558)^2
}

optimize(loss, c(100, 1000))

## $minimum
## [1] 246.4563
## 
## $objective
## [1] 8.591375e-18

Thus, according to the optimize function we need 247 participants (per group; total N = 988), to get an expected MOE equal to our target MOE. The expected MOE equals 0.4553, which you can confirm by using the MOE function we made above.

Planning with assurance

Although expected MOE is close to our target MOE, there is a probability 50% that the obtained MOE will be larger than our target MOE. In other words, repeated sampling will lead to obtained MOEs larger than what we want. That is to say, we have 50% assurance that our obtained MOE will be at least as small as our target MOE.

Planning with assurance means that we aim for a certain specified assurance that our obtained MOE will not exceed our target MOE. For instance, we may want to have 80% assurance that our obtained MOE will not exceed our target MOE.

Basically, what we need to do is take the sampling distribution of the estimate of Mean Square Error into account. We use the following formula (see also my post introducing the Precision App for the general formulae: https://the-small-s-scientist.blogspot.nl/2017/04/planning-for-precision.html).

$MOE_{\gamma} = 2*t_{.975}(df)*\sqrt{MS_w/n_i*\chi^2_{\gamma}(df)/df},$

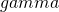where $gamma$ is the assurance expressed in a probability between 0 and 1.

Let’s do it in R. Again, the function that calculates assurance MOE is tailored for the specific situation, but it is relatively easy to formulate these functions in a generally applicable way,

MOE.gamma = function(n) {
  df = 4*(n-1)
  MOE = 2*qt(.975, df)*sqrt(3.324/n*qchisq(.80, df)/df)
}
loss <- function(n) {
  (MOE.gamma(n) - 0.4558)^2
}

optimize(loss, c(100, 1000))

## $minimum
## [1] 255.576
## 
## $objective
## [1] 2.900716e-18

Thus, according to the results, we need 256 persons per group (N = 1024 in total) to have a 80% probability of obtaining a MOE not larger than our target MOE. In that case, our expected MOE will be 0.4472.

April 21, 2017October 22, 2019

What is NHST, anyway?

I am not a fan of NHST (Null Hypothesis Significance Testing). Or maybe I should say, I am no longer a fan. I used to believe that rejecting null-hypotheses of zero differences based on the p-value was the proper way of gathering evidence for my substantive hypotheses. And the evidential nature of the p-value seemed so obvious to me, that I frequently got angry when encountering what I believed were incorrect p-values, reasoning that if the p-value is incorrect, so must be the evidence in support of the substantive hypothesis.

For this reason, I refused to use the significance tests that were most frequently used in my field, i.e. performing a by-subjects analysis and a by-item analysis and concluding the existence of an effect if both are significant, because the by-subjects analyses in particular regularly leads to p-values that are too low, which leads to believing you have evidence while you really don’t. And so I spent a huge amount of time, coming from almost no statistical background – I followed no more than a few introductory statistics courses – , mastering mixed model ANOVA and hierarchical linear modelling (up to a reasonable degree; i.e. being able to get p-values for several experimental designs). Because these techniques, so I believed, gave me correct p-values. At the moment, this all seems rather silly to me.

I still have some NHST unlearning to do. For example, I frequently catch myself looking at a 95% confidence interval to see whether zero is inside or outside the interval, and actually feeling happy when zero lies outside it (this happens when the result is statistically significant). Apparently, traces of NHST are strongly embedded in my thinking. I still have to tell myself not to be silly, so to say.

One reason for writing this blog is to sharpen my thinking about NHST and trying to figure out new and comprehensible ways of explaining to students and researchers why they should be vary careful in considering NHST as the sine qua non of research. Of course, if you really want to make your reasoning clear, one of the first things you should do is define the concepts you’re reasoning about. The purpose of this post is therefore to make clear what my “definition” of NHST is.

My view of NHST is very much based on how Gigerenzer et al. (1989) describe it:

“Fisher’s theory of significance testing, which was historically first, was merged with concepts from the Neyman-Pearson theory and taught as “statistics” per se. We call this compromise the “hybrid theory” of statistical inference, and it goes without saying the neither Fisher nor Neyman and Pearson would have looked with favor on this offspring of their forced marriage.” (p. 123, italics in original).

Actually, Fisher’s significance testing and Neyman-Pearson’s hypothesis testing are fundamentally incompatible (I will come back to this later), but almost no texts explaining statistics to psychologists “presented Neyman and Pearson’s theory as an alternative to Fisher’s, still less as a competing theory. The great mass of texts tried to fuse the controversial ideas into some hybrid statistical theory, as described in section 3.4. Of course, this meant doing the impossible.” (p. 219, italics in original).

So, NHST is an impossible, as in logically incoherent, “statistical theory”, because it (con)fuses concepts from incompatible statistical theories. If this is true, which I think it is, doing science with a small s, which involves logical thinking, disqualifies NHST as a main means of statistical inference. But let me write a little bit more about Fisher’s ideas and those of Neyman and Pearson, to explain the illogic of NHST.

I will try to describe the main characteristics of the two approaches that got hybridized in NHST at a conceptual level. I will have to simplify a lot and I hope these simplifications do little harm. Let’s start with Fisher’s significance testing.

Fisher’s significance testing

The main purpose of Fisher’s significance testing is gathering evidence about parameters in a statistical model on the basis of a sample of data. So, the nature of the approach is evidential. Crucially, the evidence the data provides can only be evidence against a statistical model, but it can not be evidence in favour of the model, much in line with Popper’s idea of progress in science by means of falsification. The statistical model to be nullified, i.e. the model one tries to obtain evidence against, is called the null-hypothesis.

Conceptually, the statistical model is a descriptive model of a population of possible values. An important part of Fisher’s approach is therefore to judge what kind of model provides an appropriate model of the population. For instance, this process of formulating the model (which, of course, involves a lot of thought and judgement) may lead one to assume that the random variable has a normal distribution, which is characterized by only two parameters, μ the expected value or mean of the distribution and σ, the square root of the variance of the distribution, which in the case of the normal distribution is it’s standard deviation (the standard deviation is the square root of the variance).

The values of μ and σ (or σ²) are generally unknown, but we may assume (again as a result of thinking and judging) that they have particular values. For reasons of exposition, I will now assume that the value of σ is known, say σ = 15, so that we only have to take the unknown value of μ into account. Let’s suppose that our thinking and judging has led us to assume that the unknown value of μ = 100. The null-hypothesis is therefore that the variable has a normal distribution with μ = 100, and σ = 15.

We can obtain evidence against this null-hypothesis, by determining a p-value. We first gather data, say we take a random sample of N = 225 participants, which enables us to obtain observed values of the variable. Next, we calculate a test statistic, for example by estimating the value of μ (on the basis of our data) subtracting the hypothesized value and dividing the estimate by it’s standard error. Our estimated value may for example be 103, and the standard error equals 15 / √225 = 1.0, so the value of the test statistic equals (103 – 100) / 1 = 3. And now we are ready to calculate the p-value.

The p-value is the probability of obtaining (when sampling repeatedly) a value of the test statistic as large as or larger than the one obtained in the study, provided that the null-hypothesis is true. This probability can be calculated because the exact distribution of the test statistic can be deduced from the specification of the null-hypothesis. In our example, the test statistic is approximately normally distributed with μ = 0, and σ = 1.0. (The distribution is approximately normal, assuming the null-hypothesis is true, so the p-value in our example not exact). The p-value equals 0.003. (This is the so-called two-sided p-value, it is the probability of obtaining a value equal or larger than 3 or equal of smaller than -3, but we will ignore the technicalities of two-sided tests).

The p-value tells us that if the null-hypothesis is true, and we repeatedly take random samples from the population (as described by the null-hypothesis) we will find a value of our test statistic or a larger value in 0.3% of these samples. Thus, the probability of obtaining a value equal to or larger than 3.0 is very small.

Following Fisher, this low p-value can be interpreted as that something “improbable” occurred (assuming the null-hypothesis is true) or as inductive evidence against the null-hypothesis, i.e. the null-hypothesis is not true.

In his early writings Fisher proposed a p-value smaller than .05 as inductive evidence against the null-hypothesis (keeping in mind the possibility that the null is true, but that something improbable happened), but later he thought using the fixed criterion of .05 to be non-scientific. If the p-value is smaller than the criterion (say .05), the result is statistically significant.

In sum, the approach by Fisher, significance testing, involves specifying a statistical model, and using the p-value to test the assumptions of the model, such as specific values for μ or σ. If the p-value is smaller than the criterion value, either something improbable occurred or the null-hypothesis is not true. Crucially, the p-value may provide inductive evidence against the assumptions of the null-hypothesis, but a large p-value (larger than the criterion value) is not inductive support for the null-hypothesis.

Neyman-Pearson hypothesis testing

In contrast to Fisher’s evidential approach, Neyman and Pearson’s hypothesis testing is non-evidential. Its primary goal is to choose on the basis of repeated random sampling between two hypotheses (or more; but I will only consider two) in order to make behavioral decisions (so to speak) that will minimize decision errors and their associated costs (loss) in the long run. In stead of trying to figure out which of the two hypotheses is true, one decides to accept one (and reject the other) of the two hypothesis as if it were true, without actually having to believe it, and act accordingly.

As with Fisher, Neyman-Pearson hypothesis testing starts with formulating descriptive models of the population. We may for instance propose (after thinking and judging) that one model (hypothesis H₁) assumes that the variable has a normal distribution with μ = 100 and one model (hypothesis H₂) that assumes that the variable has a normal distribution with μ = 106. We will assume the value of σ is known, say it equals 15. We will have to choose one of the two hypothesis, by rejecting one (and accepting the other).

Let’s suppose that only one of the models is true and that they cannot both be false. This means that we can incorrectly decide to reject or accept each of the two hypotheses. That is, if we incorrectly reject H₁, we incorrectly accept H₂. So, there are two types of errors we can make. A type I error occurs when we incorrectly reject a true hypothesis and a type II error occurs when we incorrectly accept a false hypothesis.

In a previous post (here), I used the following conceptual descriptions of these errors: the type I error is the error of excessive skepticism, and the type II error is the error of extreme gullibility, but from the perspective of Neyman-Pearson hypothesis testing these conceptual descriptions may not make much sense, because these terms imply a relation between the decisions about a hypothesis and belief in the hypothesis, while in the Neyman-Pearson approach a rejection or non-rejection does not lead to commitment in believing or not believing the hypothesis, although the hypotheses themselves are based on beliefs (and judging and reasoning) that the descriptive model is suitable for the population at hand.

The crucial point is that the goal of Neyman-Pearson hypothesis testing is to base courses of action on the decision to reject or not-reject a statistical hypothesis. This entails minimizing the costs (loss) associated with type I and type II errors. In particular, the approach minimizes the probability (β) of a type II error bounded by the probability (α) of a type I error. We may also say that we want to maximize the probability (1 – β), the probability of rejecting a false hypothesis, the so called power of the test, while keeping α at a maximum (usually low) value.

Suppose, that our considerations of the loss associated with type I and type II errors, has led us to the insight that false rejection of H₂ is the most costly error. And suppose that we have agreed/determined/reasoned/judged that the probability of falsely rejecting it should be at most .05. So, α = .05. Of course, we also “know” the loss associated with falsely accepting it, and we have determined that the probability β should not exceed .10. Now, suppose that we repeatedly sample N = 225 observations from the (unknown) population. We do not know whether H₁ or H₂ provides the correct description of the population, but we assume that one of them must be true if we select a particular sample, and they cannot both be false.

We will reject H₂ (Normal distribution with μ = 106, and σ = 15) if the sample mean in our random sample equals 104.35 or less (this corresponds to a test statistic with value -1.65). Why, because the probability of obtaining a sample mean equal or smaller than 104.35 is approximately .05 when H₂ is true. Thus, if we repeatedly sample from the population when H₂ is true, we will incorrectly reject it in 5% of the cases. Which is the probability of a type I error that we want.

We have arranged things so, that when H₂ is false, H₁ is per definition true. If H₁ is true (H₂ is false), there is a probability of approximately .99 to obtain a sample mean of 104.35 or smaller. Thus, the probability to reject H₂ when it it false is .99, this is the power of the test, and the probability is approximately .01 of incorrectly not rejecting H₂ when it is false. The latter probability is the probability of a type II error, which we did not want to be larger than .10.

Now suppose the results is that the sample mean equals 103 (the value of the test statistic equals -3). According to the decision criterion we reject H₂ (with α = .05) and accept H₁ and act as if μ = 100 is true. Crucially, we do not have to believe it is actually true, nor do we consider the test statistic with value -3 as inductive evidence against H₂. So, the test result provides neither support for H₁ nor evidence against H₂, but we know from the specification of the models and the assumptions about sampling that repeatedly using this procedure leads to 5% type I errors and 1% type II errors in the long run, depending on which of the two hypotheses is true (which is unknown to us). Given that we know the loss associated with each error, we are able to minimize the expected loss associated with acting upon the decisions we make about the hypotheses.

Note that Fisher’s significance testing would consider the p-value associated with the test statistic of -3, i.e. p < .01 either as inductive evidence against H₂ or as an indication that something unusual (improbable) happened assuming H₂ is true. Note also that in Fisher’s approach, it is not possible to reason from the inferred untruth of H₂ to the truth of H₁, because H₁ does not exist in that approach.

It should be noted further that in the Neyman-Pearson approach, the importance of the value of the test statistic is restricted to whether or not the value exceeds a critical value (i.e. whether or not the value of the statistic is in the rejection region). That means that it is of no concern how much the test statistic exceeds the critical value, since all values larger than the critical value lead to the same decision: reject the hypothesis. In other words, because the approach is non-evidential, the magnitude of the test statistic is inconsequential as far as the truth of the hypothesis is concerned. Compare this to the Fisher approach, where the larger the test statistic is (the smaller the p-value), the stronger the inductive evidence is against the null-hypothesis.

Null-hypothesis significance testing (NHST)

NHST combines Fisher’s significance testing with Neyman-Pearson hypothesis testing, without regard for the logical incompatibilities of the two approaches. Fisher’s p-value is used both as a measure of inductive evidence against the null-hypothesis, with smaller p-values considered to be stronger evidence against the null than larger p-values, and as a test statistic. In its latter use, the null-hypothesis is (usually) rejected if the p-value is smaller than .05.

Contrary to significance testing, NHST uses the p-value to decide between the null-hypothesis and an alternative hypothesis. But contrary to the Neyman-Pearson approach, α, the probability of a type I error is not based on judgement and careful consideration of loss-functions, but is mechanically set at .05 (or .01). And, contrary to the Neyman-Pearson approach, the probability of a type II error (β) is usually not considered.

One reason for the latter may be that specification of the null-hypothesis is also mechanized. In the case of differences between means or testing correlations or regression coefficients, etc, the standard null-hypothesis is that the difference, the correlation or the coefficient equals 0. This is also called the nil-hypothesis. As the alternative excludes the null, the standard alternative hypothesis is that the parameter in question is not equal to zero, which makes it hard to say something about the type II error, because determining the probability of a type II error requires thinking about a minimal consequential effect size (consequential in terms of decisions and associated loss) that can serve as the alternative hypothesis.

Specifying a non-nil alternative hypothesis, i.e. that the parameter value is not equal to zero, implies that results arbitrarily close to nil, but not equal to nil, are as consequential as effect sizes that are far away from the null-value, both in acting upon the value as in not-acting upon it. Crucially, not specifying a minimal consequential effect size, rules out determining β. So, even though NHST uses the concept of an alternative hypothesis (contrary to Fisher), the nil-hypothesis is such that the procedure of Neyman and Pearson can no longer work: it is impossible to strike a balance between loss associated with type I and type II errors, and so NHST is not a hypothesis testing procedure.

For these reasons I am very much inclined to characterize NHST as fixed-α significance testing. But using fixed-α in combination with an evidential interpretation of p-values leads to logical inconsistencies. (As always, I assume that being logically consistent is one of the characteristics of doing science, but maybe you disagree). Note, by the way, that I am talking about the p-value as measure of evidence against the nil-hypothesis, and not about the p-value as test statistic. (But remember that proper use of the p-value as test statistic requires being able to specify a non-nil alternative hypothesis).

One of the logical inconsistencies is that α and the p-value-as-evidence involve contradictory conceptualisations of probability. In terms of p-values, α is simply the probability that the p-value is smaller than .05 (the usual criterion) assuming the nil-hypothesis is true. That probability follows deductively from the specification of the null-hypothesis (including, of course, the statistical model underlying it). Note that α is completely independent of actually realized results: it an assertion about the p-value assuming repeated sampling from the null-population; α is about the test-procedure and not about actual data.

But the p-value-as-evidence against the null is not the result of deductive reasoning, but of inductive reasoning. The p-value is not a probability associated with the test-procedure. It is a random variable the value of which depends on the actual data, the null-value and the statistical model. Crucially, from a single realized result (a p-value) an inference is made about a probability distribution. But this is inconsistent with the frequency interpretation of probability that underlies the conceptualisation of α, because under this interpretation no probability statement can be made about realized single results (except that the probability is 100% that it happened) or about an unrealized single result (that probability is 0 if it does not happen or 1.0 if it happens). To make the point: using p-value-as-evidence and (fixed)-α requires both believing that probability statements can be made on the basis of a single result and believing that that is impossible. So, it boils down to believing that both A and not-A are true.

To me, logical inconsistencies like these disqualify NHST as a scientific means of statistical inference. I repeat that this is because I believe that doing science entails being logically consistent. Assuming or believing that A and not-A are both true, is not an example of logical consistency.

April 6, 2017October 22, 2019

Lazy Larry’s argument and the Mechanical Mind’s reply

Meet Lazy Larry, the non-critically thinking reviewer of your latest experimental result. (The story also applies to Lazy Larry’s reviews of non-experimental results). Lazy Larry does not believe your results signify anything “real”. Never mind your excellent experimental procedures and controls, and forget about your highly reliable instruments, Lazy Larry refuses to think about your results and by default dismisses them as “due to chance”.

“Due to chance” is simply a short-hand description of, say, your experimental group seems to outperform the control group on average, but that is not due to your experimental manipulation, but due to sampling error: you just happened to have randomly assigned better performing participants to the experimental group than to the control group.

Enter the Mechanical Mind. Its sole purpose is to persuade Lazy Larry that the results are not “due to chance”. Mechanical Mind has learned that Lazy Larry is quite easily persuaded (remember that Larry doesn’t think), so Mechanical Mind always does the following:

He pretends to have randomly assigned a random sample of participants to either the experimental or the control group. (Note the pretending is about having drawn a random sample; but since we assume an excellent experiment, we may just as well assume that the sample is in fact a random sample, but the Mechanical Mind always assumes a random sample, as part of its test procedure, even if the sample is a convenience sample).
He formulates a null-hypothesis that the mean population values are exactly equal to the millionth or more decimal.
He calculates a test statistic, say a t-value.
He determines a p-value: the probability of obtaining a t-value as large as or larger than the one obtained in the experiment, under the pretense of repeated sampling from the population, assuming the null-hypothesis is true.
He rejects the null-hypothesis if the p-value is smaller than .05 and calls that result significant.
He concludes that the results are not “due to chance” and automatically takes that conclusion to mean that the effect of the experimental manipulation is “real.”

Being a non-thinker, Lazy Larry immediately agrees: if the p-value is smaller than .05, the effect is not “due to chance”, it is a real effect.

Enter a Small s Scientist. The Small s Scientist notices something peculiar. She notices that both Lazy Larry and the Mechanical Mind do not really think, which strikes her as odd. Doesn’t science involve thinking? Here we have Larry who has only one standard argument against any experimental result, and here we have the Mechanical Mind who has only one standard reply: a mindlessly performed ritual of churning out a p-value. Yes, it may shut up Lazy Larry, if the p-value happens to be smaller than .05, but the Small s Scientist is not lazy, she really thinks about experimental results.

She wonders about Lazy Larry’s argument. We have an experiment with excellent experimental procedures and controls, with highly reliable instruments, so although sampling error always has some role to play, it doesn’t immediately come to mind as a plausible explanation for the obtained effect. Again, simply assuming this by-default, is the mark of an unthinking mind.

She thinks about the Mechanical Minds procedure. The Mechanical Mind assumes that the mean population values are completely equal up to the millionth decimal or more. Why does the Mechanical Mind assume this? Is it really plausible that it is true? To the millionth decimal? Furthermore, she realizes that she has just read the introduction section of your paper in which you very intelligently and convincingly argue that your independent variable must have a major role to play in explaining the variation in the dependent variable. But now we have to assume that the population means are exactly the same? Reading your introduction section makes this assumption highly implausible.

She recognizes that the Mechanical Mind made you do a t-test. But is the t-test appropriate in the particular circumstances of your experiment? The assumptions of the test are that you have sampled from a normally distributed population with equal variance. Do these assumptions apply? The Mechanical Mind doesn’t seem to be bothered much about these assumptions at all. How could it? It cannot think.

She notices the definition of the p-value. The probability of obtaining a value of, in this case, the t-statistic as large as or larger than the one obtained in the experiment, assuming repeated random sampling from a population in which the null-hypothesis is true. But wait a minute, now we are assigning a probability statement to an individual event (i.e. the obtained t-statistic). Can we do that? Doesn’t a frequentist conception of probability rule out assigning probabilities to single events? Isn’t the frequentist view of probability restricted to the possibly infinite collection of single events and the frequency of occurrence of the possible values of the dependent variable? Is it logically defensible to assign probabilities to single events and at the same time make use of a frequentist conception of probability? It strikes the Small s Scientist as silly to think it is.

She understands why the Mechanical Mind focuses on the probability of obtaining results (under repeated sampling from the null-population) as extreme as or extremer than the one obtained. It is simply that any obtained result has a very low probability (if not 0; e.g. if the dependent variable is continuous), no matter the hypothesis. So, the probability of a single obtained t-statistic is so low to be inconsistent with every hypothesis. But why, she wonders, do we need to consider all the results that were not obtained (i.e. the more extreme results) in determining whether a “due to chance” explanation has some plausibility (remember that the “due to chance” argument does not seem to be very plausible to begin with)? Why, she wonders, do we not restrict ourselves to the data that were actually obtained?

The Small s Scientist gets a little frustrated when thinking about why a null-hypothesis can be rejected if p < .05 and not when p > .05. What is the scientific justification of using this criterion? She has read a lot about statistics but never found a justification of using .05, apart from Fisher claiming that .05 is convenient, which is not really a justification. It doesn’t seem to be very scientific to justify a critical value simply by saying that Fisher said so. Of course, the Small s Scientist knows about decision procedures a la Neyman and Pearson’s hypothesis testing in which setting α can be done on a rational basis by considering loss functions, but considering loss functions is not part of the Mechanical Mind’s procedure. Besides, is the purpose of the Mechanical Mind’s procedure not to counter the “due to chance” explanation, by providing evidence against it, in stead of deciding whether or not the result is due to chance? In any case, the 5% criterion is an unjustified criterion, and using 5% by-default is, let’s repeat it again, the mark of an unthinking mind.

The final part of the Mechanical Mind’s procedure strikes the Small s Scientist as embarrassingly silly. Here we see a major logical error. The Mechanical Mind assumes, and Lazy Larry seems to believe, that a low p-value (according to an unjustified convention of .05) entails that results are not “due to chance” whereas a high p-value means that the results are “due to chance”, and therefore not real. Maybe it should not surprise us that unthinking minds, mechanical, lazy, or both, show signs of illogical reasoning, but it seems to the Small s Scientist that illogical thinking has no part to play in doing science.

The logical error is the error of the transposed conditional. The conditional is: If the null-hypothesis (and all other assumptions, including repeated random sampling) is/are true, the probability of obtaining a t-statistic as large as or larger than the one obtained in the experiment is p. That is, if all of the obtained t-statistics in repeated samples are “due to chance”, the probability of obtaining one as large as or larger than the one obtained in the experiment equals p. It’s incorrect transpose is: if the p-value is small, than the null-hypothesis is not true (i.e. the results are not “due to chance”). Which is very close to: If the null-hypothesis is true, these results (or more extreme results) do not happen very often” to “If these results happen, the null-hypothesis is not true”. More abstractly the Mechanical Mind goes from “If H, than probably not R” to “If R, than probably not H”, where R stands for results and H for the null-hypothesis.”.

To sum up. The Small s Scientist believes that science involves thinking. The Mechanical Mind’s procedure is an unthinking reply to Lazy Larry’s standard argument that experimental results are “due to chance”. The Small s Scientist tries to think beyond that standard argument and finds many troubling aspects of the Mechanical Mind’s procedure. Here are the main points.

The plausibility of the null-hypothesis of exactly equal population means can not be taken for granted. Like every hypothesis it requires justification.
The choice for a test statistic can not be automatically determined. Like every methodological choice it requires justification.
The interpretation of the p-value as a measure of evidence against the “due to chance” argument requires assigning a probability statement to a single event. This is not possible from a frequentist conception of probability. So, doing so, and simultaneously holding a frequentist conception of probability means that the procedure is logically inconsistent. The Small s Scientist does not like logical inconsistency in scientific work.
The p-value as a measure of evidence, includes “evidence” not actually obtained. How can a “due to chance” explanation (as implausible as it often is) be discredited on the basis of evidence that was not obtained?
The use of a criterion of .05 is unjustified, so even if we allow logical inconsistency in the interpretation of the p-value (i.e. assigning a probability statement to a single event), which a Small s Scientist does not, we still need a scientific justification of that criterion. The Mechanical Mind’s procedure does not provide such a justification.
A large p-value does not entail that the results “are due to chance”. A p-value cannot be used to distinguish “chance” results from “non-chance” results. The underlying reasoning is invalid, and a Small s Scientist does not like invalid reasoning in scientific work.

April 4, 2017November 7, 2019

Type I error probability does not destroy the evidence in your data

Have you heard about that experimental psychologist? He decided that his participants did not exist, because the probability of selecting them, assuming they exist, was very small indeed (p < .001). Fortunately, his colleagues were quick to reply that he was mistaken. He should decide that they do exist, because the probability of selecting them, assuming they do not exist, is very remote (p < .001). Yes, even unfunny jokes can be telling about the silliness of significance testing.

But sometimes the silliness is more subtle, for instance in a recent blog post by Daniel Lakens, the 20% Statistician with the title “Why Type I errors are more important than Type 2 errors (if you care about evidence).” The logic of his post is so confused, that I really do not know where to begin. So, I will aim at his main conclusion that type I error inflation quickly destroys the evidence in your data.

(Note: this post uses mathjax and I’ve found out that this does not really work well on a (well, my) mobile device. It’s pretty much unreadable).

Lakens seems to believe that the long term error probabilities associated with decision procedures, has something to do with the actual evidence in your data. What he basically does is define evidence as the ratio of power to size (i.e. the probability of a type I error), it’s basically a form of the positive likelihood ratio

$PLR = \frac{1 - \beta}{\alpha},$

which makes it plainly obvious that manipulating $\alpha$ (for instance by multiplying it with some constant c) influences the PLR more than manipulating $\beta$ by the same amount. So, his definition of “evidence” makes part of his conclusion true, by definition: $\alpha$ has more influence on the PLR than $\beta$ , But it is silly to reason on the basis of this that the type I error rate destroys the evidence in your data.

The point is that $\alpha$ and $\beta$ (or the probabilities of type I errors and type II errors) have nothing to say about the actual evidence in your data. To be sure, if you commit one of these errors, it is the data (in NHST combined with arbitrary i,e, unjustified cut-offs) that lead you to these errors. Thus, even $\alpha = .01$ and $\beta = .01$ , do not guarantee that actual data lead to a correct decision.

Part of the problem is that Lakens confuses evidence and decisions, which is a very common confusion in NHST practice. But, deciding to reject a null-hypothesis, is not the same as having evidence against it (there is this thing called type I error). It seems that NHST-ers and NHST apologists find this very very hard to understand. As my grandmother used to say: deciding that something is true, does not make it true

I will try to make plausible that decisions are not evidence (see also my previous post here). This should be enough to show you that error probabilities associated with the decision procedure tells you nothing about the actual evidence in your data. In other words, this should be enough to convince you that Type 1 error rate inflation does not destroy the evidence in your data, contrary to the 20% Statistician’s conclusion.

Let us consider whether the frequency of correct (or false) decisions is related to the evidence in the data. Suppose I tell you that I have a Baloney Detection Kit (based for example on the baloney detection kit at skeptic.com) and suppose I tell you that according to my Baloney Detection Kit the 20% Statistician’s post is, well, Baloney. Indeed, the quantitative measure (amount of Baloneyness) I use to make the decision is well above the critical value. I am pretty confident about my decision to categorize the post as Baloney as well, because my decision procedure rarely leads to incorrect decisions. The probability that I decide that something is Baloney when it is not is only $\alpha = .01$ and the probability that I decide that something is not-Baloney when it is in fact Baloney is only 1% as well ( $\beta = .01$ ).

Now, the 20% Statistician’s conclusion states that manipulating $\alpha$ , for instance by setting $\alpha = .10$ destroys the evidence in my data. Let’s see. The evidence in my data is of course the amount of Baloneyness of the post. (Suppose my evidence is that the post contains 8 dubious claims). How does setting $\alpha$ have any influence on the amount of Baloneyness? The only thing setting $\alpha$ does is influence the frequency of incorrect decisions to call something Baloney when it is not. No matter what value of $\alpha$ (or $\beta$ , for that matter) we use, the amount of Baloneyness in this particular post (i.e. the evidence in the data) is 8 dubious claims.

To be sure, if you tell the 20% Statistician that his post is Baloney, he will almost certainly not ask you how many times you are right and wrong on the long run (characteristics of the decision procedure), he will want to see your evidence. Likewise, he will probably not argue that your decision procedure is inadequate for the task at hand (maybe it is applicable to science only and not to non-scientific blog posts), but he will argue about the evidence (maybe by simply deciding (!) that what you are saying is wrong; or by claiming that the post does not contain 8 dubious claims, but only 7).

The point is, of course, this: the long term error probabilities $\alpha$ and $\beta$ associated with the decision procedure, have no influence on the actual evidence in your data. The conclusion of the 20% Statistician is simply wrong. Type I error inflation does not destroy the evidence in your data, nor does type II error inflation.

February 15, 2017October 22, 2019

Decisions are not evidence

The thinking that lead to this post began with trying to write something about what Kline (2013) calls the filter myth. The filter myth is the arguably – in the sense that it depends on who you ask – mistaken belief in NHST practice that the p-value discriminates between effects that are due to chance (null-hypothesis not rejected) and those that are real (null-hypothesis rejected). The question is whether decisions to reject or not reject can serve as evidence for the existence of an effect.

Reading about the filter myth made me wonder whether NHST can be viewed as a screening test (diagnostic test), much like those used in medical practice. The basic idea is that if the screening test for a particular condition gives a positive result, follow-up medical research will be undertaken to figure out whether that condition is actually present. (We can immediately see, by the way, that this metaphor does not really apply to NHST, because the presumed detection of the effect is almost never followed up by trying to figure out whether the effect actually exists, but the detection itself is, unlike the screening test, taken as evidence that the effect really exists; this is simply the filter myth in action).

Let’s focus on two properties of screening tests. The first property is the Positive Likelihood Ratio (PLR). The PLR is the ratio of the probability of a correct detection to the probability of a false alarm. In NHST-as-screening-test, the PLR equals the ratio of the power of the test to the probability of a type I error: PLR = (1 – β) / α. A high value of the PLR means, basically, that a rejection is more likely to be a rejection of a false null than a rejection of a true null, thus the PLR means that a rejection is more likely to be correct than incorrect.

As an example, if β = .20, and α = . 05, the PLR equals 16. This means that a rejection is 16 times more likely to be correct (the null is false) than incorrect (the null is true).

The second property I focused on is the Negative Likelihood Ratio (NLR). The NLR is the ratio of the frequency of incorrect non-detections to the frequency of correct non-detections. In NHST-as-screening-test, the NLR equals the ratio of the probability of a type II error to the probability of a correct non-rejection: NLR = β / (1 – α). A small value of the NLR means, in essence, that a non-rejection is less likely to occur when the null-hypothesis is false than when it is true.

As an example, if β = .20, and α = . 05, the NLR equals .21. This means that a non-rejection is .21 times more likely (or 4.76 (= 1/.21) times less likely) to occur when the null-hypothesis is false, than when it is true.

The PLR and the NLR can be used to calculate the likelihood ratio of the alternative hypothesis to the null-hypothesis given that you have rejected or given that you have not-rejected, the posterior odds of the alternative to the null. All you need is the likelihood ratio of the alternative to the null before you have made a decision and you multiply this by the PLR after you have rejected, and by the NLR after you have not rejected.

Suppose that we repeatedly (a huge number of times) take a random sample from a population of null-hypotheses in which 60% of them are false and 40% true. If we furthermore assume that a false null means that the alternative must be true, so that the null and the alternative cannot both be false, the prior likelihood of the alternative to the null equals p(H1)/p(H0) = .60/.40 = 1.5. Thus, of all the randomly selected null-hypotheses, the proportion of them that are false is 1.5 times larger than the proportion of null-hypotheses that are true. Let’s also repeatedly sample (a huge number of times) from the population of decisions. Setting β = .20, and α = . 05, the proportion of rejections equals p(H1)*(1 – β) + p(H0)*α = .60*.80 + .40*.05 = .50 and the proportion of non-rejections equals p(H1)*β + p(H0)*(1 – α) = .60*.20 + .40*.95 = .50. Thus, if we sample repeatedly from the population of decisions 50% of them are rejections and 50% of them are non-rejections.

First, we focus only on the rejections. So, the probability of a rejection is now taken to be 1.0. The posterior odds of the alternative to the null, given that the probability of a rejection is 1.0, is the prior likelihood ratio multiplied by the PLR: 1.5 * 16 = 24. Thus, we have a huge number of rejections (50% of our huge number of randomly sampled decisions) and within this huge number of rejections the proportion of rejections of false nulls is 24 times larger than the proportion of rejections of true nulls. The proportion of rejections of false nulls equals the posterior odds / (1 + posterior odds) = 24 / 25 = .96. (Interpretation: If we repeatedly sample a null-hypothesis from our huge number of rejected null-hypotheses, 96% of those samples are false null-hypotheses).

Second, we focus only on the non-rejections. Thus, the probability of a non-rejection is now taken to be 1.0. The posterior odds of the alternative to the null, given that the probability of a non-rejection is 1.0, is the prior odds multiplied by the NLR: 1.5 * 0.21 = 0.32. In other words, we have a huge number of non-rejections (50% of our huge sample of randomly selected decisions) and the proportion of non-rejections of false nulls is 0.32 times as large as the proportion of non-rejections of true nulls. The proportion of non-rejections of false nulls equals 0.32 / ( 1 + 0.32) = .24. (Interpretation: If we repeatedly sample a null-hypothesis from our huge number of non-rejected hypotheses, 24% of them are false nulls).

So, based on the assumptions we made, NHST seems like a pretty good screening test, although in this example NHST is much better at detecting false null-hypothesis than ruling out false alternative hypotheses. But how about the question of decisions as evidence for the reality of an effect? I will first write a little bit about the interpretation of probabilities, then I will show you that decisions are not evidence.

Sometimes, these results are formulated as follows. The probability that the alternative is true given a decision to reject is .96 and the probability that the alternative hypothesis is true given a decision to not-reject is .24. If you want to correctly interpret such a statement, you have to keep in mind what “probability” means in the context of this statement, otherwise it is very easy to misinterpret the statement’s meaning. That is why I included interpretations of these results that are consistent with the meaning of the term probability as it used in our example. (In conceptual terms, the limit of the relative frequency of an event (such as reject or not-reject) as the number of random samples (the number of decisions) goes to infinity).

A common (I believe) misinterpretation (given the sampling context described above) is that rejecting a null-hypothesis makes the alternative hypothesis likely to be true. This misinterpretation is easily translated to the incorrect conclusion that a significant test result (that leads to a rejection) makes the alternative hypothesis likely to be true. Or, in other words, that a significant result is some sort of evidence for the alternative hypothesis (or against the null-hypothesis).

The mistake can be described as confusing the probability of a single result with the long term (frequentist) probabilities associated with the decision or estimation procedure. For example, the incorrect interpretation of the p-value as the probability of a type I error or the incorrect belief that an obtained 95% confidence interval contains the true value of a parameter with probability .95.

A quasi-simple example may serve to make the mistake clear. Suppose I flip a fair coin, keep the result hidden from you, and let you guess whether the result is heads or tails (we assume that the coin will not land on it’s side). What is the probability that your guess is correct?

My guess is that you believe that the probability that your guess is correct is .50. And my guess is also that you will find it hard to believe that you are mistaken. Well, you are mistaken if we define probabilities as long term relative frequencies. Why? The result is either heads or tails. If the result is heads, the long term relative frequency of that result is heads. That is to say, the result is a constant and constants do not vary in the long run. Your guess is also a constant, if you guess heads, it will stay heads in the long run. So, if the result is heads, the probability that your guess (heads) is correct is 100%, however, if your guess is tails, the probability of you being correct is 0%. Likewise, if the result is tails, it will stay tails forever, and the probability that your guess is correct is 0% if your guess is heads and 100% if your guess is tails. So, the probability that your guess is correct is either 0 or 1.0, depending on the result of the coin flip, and not .50.

The probability of guessing correct is .50, however, if we repeatedly (a huge number of times) play our game and both the result of the coin flip and your guess are the result of random sampling. Let’s assume that of all the guesses you do 50% are heads and 50% are tails. In the long run, then, there is a probability of .25 of the result being heads and your guess being heads and a probability of .25 of the result being tails and your guess being tails. The probability of a correct decision is therefore, .25 + .25 = .50

Thus, if both the results and your guesses are the result of random sampling and we repeated the game a huge number of times, the probability that you are correct is .50. But if we play our game only once, the probability of you being correct is 0 or 1.0, depending on the result of the coin flip.

Let’s return to the world of hypotheses and decisions. If we play the decision game once, the probability that your decision is correct is 0 or 1.0, depending on whether the null-hypothesis in question is true (with probability 0 or 1.0) or false (with probability 0 or 1.0). Likewise, the probability that the null-hypothesis is true given that you have rejected is also 0 or 1.0, depending on whether the null-hypothesis in question is true or false. But if we play the decision game a huge number of times, the probability that a null-hypothesis is false, given that you have decided to reject is .96 (in the context of the situation described above).

In sum, from the frequentist perspective we can only assign probabilities 0 or 1.0 to a single hypothesis given we have a made single decision about it, and this probability depends on whether that single hypothesis is true or false. For this reason, a significant result cannot be magically translated to the probability that the alternative hypothesis is true given that the test result is significant. That probability is 0 or 1.0 and there’s nothing that can change that.

The consequence of all this is as follows. If we define the evidence for or against our alternative hypothesis in terms of the likelihood ratio of the alternative to the null-hypothesis after obtaining the evidence, no decision can serve as evidence if our decision procedure is based on frequentist probabilities. Decisions are not evidence.

References
Kline, R.B. (2013). Beyond significance testing. Statistics reform in the behavioral sciences. Second Edition. Washington: APA.