Planning for Precision: first simulation results

In this post, I want to share the results of the first simulation study to “test” my Planning for Precision app. More details about the app can be found in a previous post: here.

I have included the basic logic of the simulations (including R code) in a document that you can download: https://drive.google.com/open?id=0B4k88F8PMfAhSlNteldYRWFrQTg.

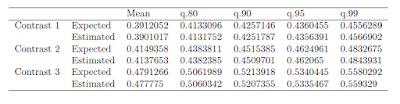
The simulation study simulates responses from a four condition counter balanced design, with p = 48 participants and q = 24 stimuli/items. Here, we will focus on expected and assurance MOE for three contrasts. The first contrast estimates the difference between the first mean and the average of the other three, the second contrast the difference between the second mean and the average of the third and fourth means, and the final contrast the difference between the means of the third and fourth contrasts.

Expected MOE is compared to the mean of the estimated MOE for each of the contrasts (based on 10000 replications). Assurance MOE is judged for assurance of .80, .90, .95 and .99, by comparing the calculations in the app with the corresponding quantile estimates of the simulated distributions.

Results

Note that in the above table, the Expected Mean MOE is what I have called Expected MOE, and the q.80 through q.99 are quantiles of the distribution of MOE. As an example, q.80 is the quantile corresponding to assurance MOE with 80% assurance, Expected q.80 is the value of assurance MOE calculated with the theoretical approach, and Estimated q.80 is the estimated quantile based on the simulation studies.

Importantly, we can see that most of the figures agree to a satisfying degree. If we look at the relative differences, expressed in percentages for the assurance MOEs, we get 0.0325% for q.80, 0.1260% for q.90, 0.0933% for q.95, and -0.2324% for q.99.

Conclusion

The first simulation results seem promising. But I still have a lot of work to do for the rest of the designs.