MOE Archives - The small S scientist

March 22, 2019October 22, 2019

Planning with assurance, with assurance

Planning for precision requires that we choose a target Margin of Error (MoE; see this post for an introduction to the basic concepts) and a value for assurance, the probability that MoE will not exceed our target MoE. What your exact target MoE will be depends on your research goals, of course.

Cumming and Calin-Jageman (2017, p. 277) propose a strategy for determining target MoE. You can use this strategy if your research goal is to provide strong evidence that the effect size is non-zero. The strategy is to divide the expected value of the difference by two, and to use that result as your target MoE.

Let’s restrict our attention to the comparison of two means. If the expected difference between the two means is Cohens’s d = .80, the proposed strategy is to set your target MoE at f = .40, which means that your target MoE is set at .40 standard deviations. If you plan for this value of target MoE with 80% assurance, the recommended sample size is n = 55 participants per group. These results are guaranteed to be true, if it is known for a fact that Cohen’s d is .80 and all statistical assumptions apply.

But it is generally not known for a fact that Cohen’s d has a particular value and so we need to answer a non-trivial question: what effect size can we reasonably expect? And, how can we have assurance that the MoE will not exceed half the unknown true effect size? One of the many options we have for answering this question is to conduct a pilot study, estimate the plausible values of the effect size and use these values for sample size planning. I will describe a strategy that basically mirrors the sample size planning for power approach described by Anderson, Kelley, and Maxwell (2017).

The procedure is as follows. In order to plan with approximately 80% assurance, estimate on the basis of your pilot the 80% confidence interval for the population effect size and use half the value of the lower limit for sample size planning with 90% assurance. This will give you 81% assurance that assurance MoE is no larger than half the unknown true effect size.

The logic of planning with assurance, with assurance

There are two “problems” we need to consider when estimating the true effect size. The first problem is that there is at least 50% probability of obtaining an overestimate of the true effect size. If that happens, and we take the point estimate of the effect size as input for sample size planning, what we “believe” to be a sample size sufficient for 80% assurance will be a sample size that has less than 80% assurance at least 50% of the times. So, using the point estimate gives assurance MoE for the unknown effect size with less than 50% assurance.

To make it more concrete: suppose the true effect equals .80, and we use n = 25 participants in both groups of the pilot study, the probability is approximately 50% that the point estimate is above .80. This implies, of course, that we will plan for a value of f > .40, approximately 50% of the times, and so the sample we get will only give us 80% assurance 50% of the times.

The second problem is that the small sample sizes we normally use for pilot studies may give highly imprecise estimates. For instance, with n = 25 participants per group, the expected MoE is f = 0.5687. So, even if we accept 50% assurance, it is highly likely that the point estimate is rather imprecise.

Since we are considering a pilot study, one of the obvious solutions, increasing the sample size so that expected MoE is likely to be small, is not really an option. But what we can do is to use an estimate that is unlikely to be an overestimate of the true effect size. In particular, we can use as our estimate the lower limit of a confidence interval for the effect size.

Let me explain, by considering the 80% CI of the effect size estimate. From basic theory it follows that the “true” value of the effect size will be smaller than the lower limit of the 80% confidence interval with probability equal to 10%. That is, if we calculate a huge number of 80% confidence intervals, each time on the basis of new random samples from the population, the true value of the effect size will be below the lower limit in 10% of the cases. This also means that the lower limit of the interval has 90% probability to not overestimate the true effect size.

This means that if we take the lower limit of the 80% CI of the pilot estimate as input for our sample size calculations, and if we plan with assurance of .90, we will have 90%*90% = 81% assurance that using the sample size we get from our calculations will have MoE no larger than half the true effect size. (Note that for 80% CI’s with negative limits you should choose the upper limit).

Sample Size planning based on a pilot study

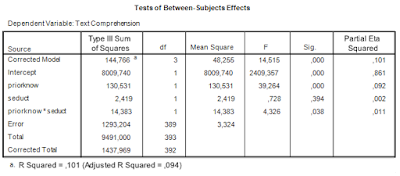
Student of mine recently did a pilot study. This was a pilot for an experiment investigating the size of the effect of fluency of delivery of a spoken message in a video on Comprehensibility, Persuasiveness and viewers’ Appreciation of the video. The pilot study used two groups of size n = 10, one group watched the fluent video (without ‘eh’) and the other group watched the disfluent video where the speaker used ‘eh’ a lot. The dependent variables were measured on 7-point scales.

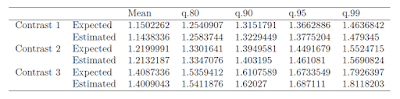
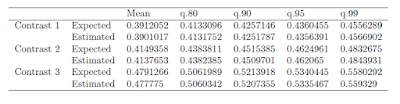
Let’s look at the results for the Appreciation variable. The (biased) estimate of Cohen’s d (based on the pooled standard deviation) equals 1.09, 80% CI [0.46, 1.69] (I’ve calculated this using the ci.smd function from the MBESS-package. According to the rules-of-thumb for interpreting Cohen’s d, this can be considered a large effect. (For communication effect studies it can be considered an insanely large effect). However, the CI shows the large imprecision of the result, which is of course what we can expect with sample sizes of n = 10. (Average MoE equals f = 0.95, and according to my rules-of-thumb that is well below what I consider to be borderline precise).

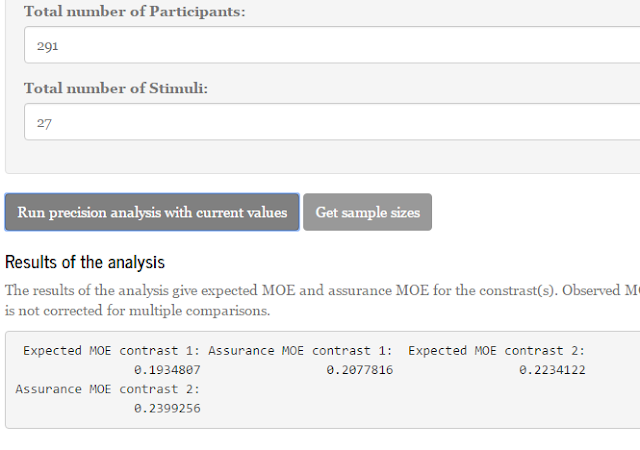
If we use the lower limit of the interval (d = 0.46), sample size planning with 90% assurance for half that effect (f = 0.23) gives us a sample size equal to n = 162. (Technical note: I planned for the half-width of the standardized CI of the unstandardized effect size, not for the CI of the standardized effect size; I used my Shiny App for planning assuming an independent groups design with two groups). As explained, since we used the lower limit of the 80% CI of the pilot and used 90% assurance in planning the sample size, the assurance that MoE will not exceed half the unknown true effect size equals 81%.

June 21, 2018October 22, 2019

A rule of thumb for setting target MOE

One of the most difficult aspects of sample size planning for precision is the specification of a target Margin of Error (MoE). Here, I would like to introduce a simple rule of thumb, in the hope that it helps you in determining a reasonable target MoE.
Here, the rule of thumb is applied to obtaining an estimate of the difference between two independent group means, where the two populations are normally distributed with equal variances.

Goal 1: Assessing the direction of an effect

Sample size planning starts with formulating a goal for the research. A very common goal is to try to determine the direction of an effect. For the goal of assessing the direction of an effect, it helps if the confidence interval of the difference contains only positive or negative values. That is, you want a confidence interval that exludes the value 0, for if that value is included, you would probably conclude that the estimate is consistent with both positive and negative effects. Thus, our first goal is to obtain a confidence interval of the mean difference that excludes the value 0.

Now, a confidence interval excludes 0, if obtained MOE is at most equal to the obtained effect size estimate. Suppose that the estimate equals the true effect of say, 0.50, we want MOE to be at most very close to 0.50, otherwise 0 will be included in the interval. But if our estimate underestimates the true effect, say the estimate equals 0.30, we want MOE to be at most very close to 0.30. Likewise, if we overestimate the effect, MOE can be larger than 0.50.

This means that we cannot say, for instance, we expect that the true effect is .50, so let’s plan for a target MOE that with 80% assurance is at most .50, because this target MOE may be too large for underestimates of the true effect, depending on the extent to which the effect is underestimated. So, in specifying target MOE, we should take into account that underestimates of the effect size occur. (Actually, these underestimates occur with a relative frequency of 50% in a huge collection of direct replications). We can say that we do not only want to exclude zero from the interval, but also that we want that to occur in a large proportion of direct replications. This will be our second goal. I will call the probabiity associated with our second goal, the probability of exclusion (PE)

The rule of thumb is that if we want 80% probability that a random confidence interval excludes zero, we should plan for an expected MOE equal to f = d / √2. (the square root sign is unreadable in my browser; so in words: the effect size divided by the square root of 2; with mathjax: $f = d / sqrt{2}$). Since there is 50% probability that obtained MOE will be larger than expected MOE, this is equal to planning for target MOE = f = d / √2, with 50% assurance or simply without assurance. You can do this in the ESCI-software, but also with the R-functions provided below.

The first example in the code below, is an illustration of planning for assessing the direction of the effect, with true effect size d = .50. If we want 80% assurance to have only positive values in our confidence interval, we should plan for a target MoE = expected MoE = f = d / √2 = 0.3535. Using the SampleSize-function below, this gives a sample size n = 63, or total sample size = N = 2*63 = 126. The probability that the confidence interval excludes 0 equals approximately 80% (p = 0.7951). So, the rule of thumb of planning for d / √2, seems to work pretty good.

Goal 2: distinguishing between effect sizes

If your research goal is to estimate the value of the effect size in stead of its direction, the rule of thumb can be used as follows. Suppose we do not know the true effect size, but want to have 80% assurance that we have a high probability to be able to distinguish between small (d = .20) and large effects (d = .80). That is, if the true effect is .20 we want the value .80 to be excluded from the confidence interval and if the true effect is .80, we want the value .20 to be excluded from the confidence interval.

We can proceed as follows, the difference between the effect sizes is .80 – .20 = .60. We use this value to determine target MOE. Thus, if we now plan for a target MoE = expected Moe = d / √2), we should have approximately 80% PE that obtained MoE will exclude 0.80 if the true effect is 0.20 and vice versa. The functions below give sample size n = 44, and the probablity of exclusion equals .7947. So, our rule of thumb, seems to work pretty good again. See example 2 in the code below.

Alternatively, we could take the region of practical equivalence (ROPE) into account. Suppose, our equivalence range equals .10 sigma. If we want to have enough precision to distinguish large from small effects, we should plan as follows. We take the difference between a large effect and the upper equivalence value of a small effect or, equivalently, the difference between a small effect and the lower equivalence vaue of a large effect, i.e. .50, and plan for f = .50 / √2. If the effect is large we expect a confidence interval that excludes the equivalence range for the small effect (and vice versa), with 80% probability of exclusion.

But we could also take the difference between the lower equivalence value of a large effect and the upper equivalence value of a small effect, i.e. .40, and plan for f = .40/√2. (See the third example in the code below) This will give us 80% PE that any true value within the ROPE of the one effect will exclude values in the ROPE of the other. For example, if the true effect is .70, and expected MOE equals .40/√2 = .2828, there is approximately 80% probability that the 95% CI excludes .30, which is in the ROPE of a small effect. The expected CI will be .70 +/- .2828 = [0.4172, 0.9828]. Note that the lower limit is larger than the upper limit of the ROPE for d = .20, as we want it to be. Note, however, that if the true effect is small (d = .20), the CI will exclude effects equivalent to large effects, which is consistent with our research goal, but it will not exlude the value 0 or effects equivalent to a medium effect. Indeed, the expected CI will be [-0.0828, 0.4828]. (This is not a problem, of course, since this was not the purpose of our research)

As a final example, suppose we want sufficient precision to distinguish small from medium effects (or large from medium effects). If we take the ROPE perspective, with an equivalence range of +/- .10 sigma, the lower equivalence value of the medium effect equals .50 – .10 = .40 and the upper limit of the small effect equals .30. If we want 80% assurance that the CI will be small enough to distinguish small from medium effects, we should plan for expected MOE f = (.40 – .30)/√2 = 0.0707. Using the functions below, this requires a sample size n = 1538. (See the final example in the code below).

Setting target MOE: conclusion

In summary, the rule of thumb is to divide the effect size d by √2 and plan for an expected MoE equal to this value. This will give you a sample size that gives approximately 80% assurance that the CI will not contain 0. In the case of distinguishing effect sizes, one option is to divide the difference between the lower equivalence value of the larger effect and the upper equivalence value of the smaller effect by the square root of 2 and plan for an expected MoE equal to this value. This will give you a sample size that gives approximately 80% PE that the CI of the estimated true value of one effect excludes the values in the ROPE of the other effect.

Do you want at least 90% PE? Use the square root of three, in stead of the square root of two, in determining target MoE.

eMoe = function(n) {
eMoe = qt(.975, 2*(n - 1))*sqrt(2/n)
return(eMoe)
}

cost <- function(n, tMoe) {
(eMoe(n) - tMoe)^2
}

sampleSize <- function(tMoe) {
optimize(cost, interval=c(10, 5000), tMoe = tMoe)$minimum
}

# FIRST EXAMPLE
# plan for 80% assurance of excluding 0
# i.e. estimate the direction if true effect
# equals .50 

d = .50

#application of rule of thumb:
f = .50 / sqrt(2)

#sampleSize (uses ceiling() to round up): 
n = ceiling(sampleSize(f))
n

## [1] 63

# Probabiity of Exclusion (here taken to be equivalent to
# power for two-sided t-test (since true direction is unknown))
df = 2*(n - 1)
ncp = f / sqrt(1/n) #or ncp = d / sqrt(2/n)

pt(qt(.025, df), df, ncp) + 1 - pt(qt(.975, df), df, ncp)

## [1] 0.7951683

# SECOND EXAMPLE: 
# distinguish between small and large effect sizes: 
d = .80 - .20
f = d / sqrt(2)

n = ceiling(sampleSize(f))
n

## [1] 44

df = 2*(n - 1)
ncp = f / sqrt(1/n) #or ncp = d / sqrt(2/n)

#PE: 

pt(qt(.025, df), df, ncp) + 1 - pt(qt(.975, df), df, ncp)

## [1] 0.79467

# EXAMPLE 3: distinguish small and large with ROPE
# ROPE small and large: 
rope.small = c(.10, .30)
rope.large = c(.70, .90)

d = rope.large[1] - rope.small[2]
f = d / sqrt(2)

n = ceiling(sampleSize(f))

n

## [1] 98

df = 2*(n - 1)
ncp = f / sqrt(1/n) #or ncp = d / sqrt(2/n)

#PE: 

pt(qt(.025, df), df, ncp) + 1 - pt(qt(.975, df), df, ncp)

## [1] 0.7956414

# Example 4: distinguish medium from small 
# or medium from large with ROPE

rope.medium = c(.40, .60)
d = rope.medium[1] - rope.small[2]
f = d / sqrt(2)

n = ceiling(sampleSize(f))

n

## [1] 1538

df = 2*(n - 1)
ncp = f / sqrt(1/n) #or ncp = d / sqrt(2/n)

#PE:

pt(qt(.025, df), df, ncp) + 1 - pt(qt(.975, df), df, ncp)

## [1] 0.7916783

March 16, 2018October 22, 2019

Sample size planning for precision: the basics

In this post, I will introduce some of the ideas underlying sample size planning for precision. The ideas are illustrated with a shiny-application which can be found here: https://gmulder.shinyapps.io/PlanningApp/. The app illustrates the basic theory considering sample size planning for two independent groups. (If the app is no longer available (my allotted active monthly hours are limited on shinyapps.io), contact me and I’ll send you the code).

The basic idea

The basic idea is that we are planning an experiment to estimate the difference in population means of an experimental and a control group. We want to know how many observations per group we have to make in order to estimate the difference between the means with a given target precision.

Our measure of precision is the Margin of Error (MOE). In the app, we specify our target MOE as a fraction (f) of the population standard deviation. However, we do not only specify our target MOE, but also our desired level of assurance. The assurance is the probability that our obtained MOE will not exceed our target MOE. Thus, if the assurance is .80 and our target MOE is f = .50, we have a probability of 80% that our obtained MOE will not exceed f = .50.

The only part of the app you need for sample size planning is the “Sample size planning”-form. Specify f, and the assurance, and the app will give you the desired sample size.

If you do that with the default values f = .50 and Assurance = .80, the app will give you the following results on the Planning Results-tab: Sample Size: 36.2175, Expected MOE (f): 0.46. This tells you that you need to sample 37 participants (for instance) per group and then the Expected MOE (the MOE you will get on average) will equal 0.46 (or even a little less, since you sample more than 36.2175 participants).

The Planning-Results-tab also gives you a figure for the power of the t-test, testing the NHST nil-hypothesis for the effect size (Cohen’s d) specified in the “Set population values”-form. Note that this form, like the rest of the app provides details that are not necessary for sample size planning for precision, but make the theoretical concepts clear. So, let’s turn to those details.

The population

Even though it is not at all necessary to specify the population values in detail, considering the population helps to realize the following. The sample size calculations and the figures for expected MOE and power, are based on the assumption that we are dealing with random samples from normal populations with equal variances (standard deviations).

From these three assumptions, all the results follow deductively. The following is important to realize: if these assumptions do not obtain, the truth of the (statistical) conclusions we derive by deduction is no longer guaranteed. (Maybe you have never before realized that sample size planning involves deductive reasoning; deductive reasoning is also required for the calculation of p-values and to prove that 95% confidence intervals contain the value of the population parameter in 95% of the cases; without these assumptions is it uncertain what the true p-value is and whether or not the 95% confidence interval is in fact a 95% confidence interval).

In general, then, you should try to show (to others, if not to yourself) that it is reasonable to assume normally distributed populations, with equal variances and random sampling, before you decide that the p-value of your t-test, the width of your confidence interval, and the results of sample size calculations are believable.

The populations in the app are normal distributions. By default, the app shows two such distributions. One of the distributions, the one I like to think about as corresponding to the control condition, has μ = 0, the other one has μ = 0.5. Both distributions have a standard deviation (σ = 1). The standardized difference between the means is therefore equal to δ = 0.50.

The default populations are presented in Figure 1 below.

Figure 1: Two normal distributions. The distribution to the left has μ = 0, the one to the right has μ = 0.5 The standard deviation in both distributions equals σ = 1. The standardized difference δ and the unstandardized difference between the means both equal 0.50.

The sampling distribution of the mean difference

The other default setting in the app is a sample size (per group) of n = 20. From the sample size and the specification of the populations, we can deduce the probability density of the different values of the estimates of the difference between the population means. The estimate is simply the difference between the sample means.

This so-called sampling distribution of the mean difference is depicted on the tab next to the population. Figure 2 shows what the sampling distribution looks like if we repeatedly draw random samples of size n = 20 per group from our populations and keep track of the difference between the sample means we get in each repetition.

Figure 2: Sampling distribution of the difference between two sample means based on samples of n = 20 per group and random sampling from the populations described in Figure 1.

Note that the mean of the sampling distribution equals 0.5 (as indicated by the middle vertical line). This is of course the (default) difference between the population means in the app. So, on average, estimates of the population difference equal the population difference.

The lines to the left and the right of the mean indicate the mean plus or minus the Margin of Error (MOE). The values corresponding to the lines are 0.5 ± MOE. 95% of estimates of the population mean difference have a value between these lines.

Conceptually, the purpose of planning for precision is to decrease the (horizontal) distance between these lines and the population mean difference. In other words, we would like the left and right lines as close to the mean of the distribution as is practically acceptable and possible.

The distribution of the t-statistic

The tab next to the sampling distribution tab contains a figure representing the sampling distribution of the t-statistic. The sampling distribution of t can be deduced on the basis of the population values and the sample size. In the app, it is assumed that t is calculated under the assumption that the null-hypothesis of zero difference between the means is true. The sampling distribution of t is what you get if you repeatedly sample from the populations as specified, calculate the t-statistic and keep a record of the values of the t-statistic.

The sampling distribution of the t-statistic presented in Figure 3 contains two vertical lines. These lines are located (horizontally) on the value of t that would lead to rejection of the null-hypothesis of equal population means. In other words, the lines are located at the critical value of t (for a two-tailed test).

Figure 3: Distribution of the t-statistic testing the null-hypothesis of equal population means. The distribution is based on sampling from the populations described in Figure 3. The sample size is n = 20 per group. The lines represent the critical value of t for a two sided t-test. The area between the vertical lines is the probability of a type II error. The combined areas to the left of the left line and to the right of the right line is the power of the test.

The area between the lines is the probability that the null-hypothesis will not be rejected. In the case of a true population mean difference (which is the default assumption in the app), that probability is the probability of an error of the second kind: a type II error.

The complement of that probability is called the power of the test. This is, of course, the area to the left of the left vertical line added to the area to the right of the right vertical line. Conceptually, the power of the test is the probability of rejecting the null-hypothesis when in fact it is false.

Figure 3 clearly demonstrates that if the true mean difference equals 0.50 and the sample size (per group) equals n = 20, that there is a large probability that the null-hypothesis will not be rejected. Actually, the probability of a type II error equals .66. (So, the power of the test is .34).

Sample size planning for precision

With respect to sample size planning for precision, the app by default takes half of a standard deviation (f = .50) as the target MOE. Besides, planning is with 80% assurance. This means that the default settings search for a sample size (per group), so that with 80% probability MOE will not exceed 0.50 (Note that the default value of the standard deviation is 1, so an f of .50 corresponds to a target MOE of 0.50 on the scale of the data; Likewise, were the standard deviation equal to 2, an f of .50 would correspond to a target MOE of 1.0).

As described above, planning with the default values gives us a sample size of n = 37 per group, with an expected MOE of 0.46. In the tab next to the planning results, a figure displays what you can expect to find on average, given the planned sample size and the specification of the population. That figure is repeated here as Figure 4.

Figure 4: Expected results in terms of point and interval estimates (95% confidence intervals). This is what you will find on average given the population specification in Figure 1 and using the default values for sample size planning.

Figure 4 displays point and interval estimates of the group means and the difference between the means. The interval estimates are 95% confidence intervals. The figure clearly shows that on average, our estimate of the difference is very imprecise. That is, the expected 95% confidence interval ranges from almost 0 (0.50 – 0.46 = 0.04) to almost 1 (0.50 + 0.46 = 0.96). Of course, using n = 20, would be worse still.

A nice thing about the app (well, I for one think it’s pretty cool) is that as soon as you ask for the sample sizes, the sample size in the set population values form is automatically updated. Most importantly, this will also update the sampling distribution graphs of the difference between the means and the t-statistic. So, it provides an excellent way of showing what the updated sample size means in terms of MOE and the power of the t-test.

Let’s have a look at the sampling distribution of the mean difference, see Figure 5.

Sampling distribution of the difference.

Figure 5: Sampling distribution of the mean difference with n = 37 per group. Compare with Figure 2 to see the (small) difference in the Margin of Error compared to n = 20.

If you compare Figures 5 and 2, you see that the vertical lines corresponding to the mean plus and minus MOE have shifted somewhat towards the mean. So here you can see, that almost doubling the sample size (from 20 to 37) had the desired effect of making MOE smaller.

I would like to point out the similarity between the sampling distribution of the difference and the expected results plot in Figure 4. If you look at the expected results for our estimate of the population difference, you see that the point estimate corresponds to the mean of the sampling distribution, which is of course equal to the populations mean difference and that the limits of the expected confidence interval correspond to the left and right vertical lines in Figure 5. Thus, on average the limits of the confidence interval correspond to the values that mark the middle 95% of the sampling distribution of the samples mean difference.

Since we specified an assurance of 80%, there is an 80% probability that in repeated sampling from the populations (see Figure 1) with n = 37 per group, our (estimated) MOE will not exceed half a standard deviation. Thus, whatever the true value of the populations mean difference is, there is a high probability that our estimate will not be more than half a standard deviation away from the mean. This is, I think, one of the major advantages of sample size planning for precision: we do not have to specify the unknown population mean difference. This is in contrast to sample size planning for power, where we do have to specify a specific population mean difference.

Speaking of power, the results of the sample size planning suggest that for our specification of the populations mean difference (Cohen’s delta = 0.50) the power of the test equals 0.56. Thus, there is a probability of 56% that with n = 37 per group the t-test will reject. The probability of a type II error is therefore 44%.

Figure 6 shows the distribution of the t statistic with n = 37 per group and a standardized effect size of 0.50.

Figure 6. The distribution of the t-statistic testing the null-hypothesis of equal population means. The distribution is based on the population specification in Figure 1 and sample sizes of n = 37 per group, with true effect size equal to 0.50. The probability of a type II error is the area of under the curve between the two vertical lines. The power is the area under the curve beyond the two lines. Compare with Figure 3 to see the differences in these probabilities compared to n = 20.

Power versus precision

Now suppose that the unstandardized mean difference between the population means equals 2 and that the standard deviation equals 2.5. I just filled in the set population values form, setting the mean of population 2 to 2.0 and the standard deviation to 2.5. And I clicked set values.

Let us plan for a target MOE of f = 0.5 standard deviations with 80% assurance. Click get sample sizes in the sample size planning form. In this case, target MOE equals 1.25.

The results are not very surprising. Since the f did not change compared to the previous time, the results as regards the sample size are exactly the same. We need n = 37. Again, this is what I like about sample size planning, no matter what the unknown situation in the population is, I just want my margin of error to be no more than half a standard deviation (for example).

But the power did change (of course). Since the standardized population mean difference is now 0.80 (= 2.0 / 2.5) in stead of 0.50, and all the other specifications remained the same, the power increases from 56% to 92%. That’s great.

However, the high probability of rejecting the null-hypothesis does not mean that we get precise estimates. On average, the point estimate of the difference equals 2 and the 95% confidence limits are 0.85 and 3.15 (the point estimate plus or minus 0.46 times the standard deviation of 2.5). See Figure 7.

Expected results large standardized effect

Figure 7: Expected results using n = 37 when sampling from two normal populations with equal standard deviations (σ = 2.5) and mean difference of 2.0. The standardized effect size equals 0.80. Note the imprecision of the estimates even though the power of the t-test equals .92.

In short, even though there is a high probability of (correctly) rejecting the null-hypothesis of equal population means, we are still not in the position to confidently conclude what the size of the difference is: the expected confidence interval is very wide.

October 9, 2017November 7, 2019

Planning for a precise slope estimate in simple regression

In this post, I will show you a way of determining a sample size for obtaining a precise estimate of the slope $\beta_1$ of the simple linear regression equation $\hat{Y_i} = \beta_0 + \beta_1X_i$ . The basic ingredients we need for sample size planning are a measure of the precision, a way to determine the quantiles of the sampling distribution of our measure of precision, and a way to calculate sample sizes.

As our measure of precision we choose the Margin of Error (MOE), which is the half-width of the 95% confidence interval of our estimate (see: Cumming, 2012; Cumming & Calin-Jageman, 2017; see also www.thenewstatistics.com).

The distribution of the margin of error of the regression slope

In the case of simple linear regression, assuming normality and homogeneity of variance, MOE is $t_{.975}\sigma_{\hat{\beta_1}}$ , where $t_{.975}$ , is the .975 quantile of the central t-distribution with $N - 2$ degrees of freedom, and $\sigma_{\hat{\beta_1}}$ is the standard error of the estimate of $\beta_1$ .

An expression of the squared standard error of the estimate of $\beta_1$ is $\frac{\sigma^2_{Y|X}}{\sum{(X_i - \bar{X})}^2}$ (Wilcox, 2017): the variance of Y given X divided by the sum of squared errors of X. The variance $\sigma^2_{Y|X}$ equals $\sigma^2_y(1 - \rho^2_{YX})$ , the variance of Y multiplied by 1 minus the squared population correlation between Y and X, and it is estimated with the residual variance $\frac{\sum{(Y -\hat{Y})^2}}{df_e}$ , where $df_e = N - 2$ .

The estimated squared standard error is given in (1)

(1) $\hat{\sigma}_{\hat{\beta_{1}}}^{2}=\frac{\sum(Y-\hat{Y})^{2}/df_{e}}{\sum(X-\bar{X})^{2}}.$

With respect to the sampling distribution of MOE, we first note the following. The distribution of estimates of the residual variance in the numerator of (1) is a scaled $\chi^2$ -distribution:

$\frac{\sum(Y-\hat{Y})^{2}}{\sigma_{y}^{2}(1-\rho^{2})}\sim\chi^{2}(df_{e}),$

thus

$\frac{\sum(Y-\hat{Y})^{2}}{df_{e}}\sim\frac{\sigma_{y}^{2}(1-\rho^{2})\chi^{2}(df_{e})}{df_{e}}.$

Second, we note that

$\frac{\sum(X-\bar{X})^{2}}{\sigma_{X}^{2}}\sim\chi^{2}(df),$

where $df = N - 1$ , therefore

$\sum(X-\bar{X})^{2}\sim\sigma_{X}^{2}\chi^{2}(df).$

Alternatively, since $\sum{(X - \bar{X})^2} = df\sigma^2_X$ , and multiplying by 1 ( $\frac{df}{df}$ ).

$df\sigma_{X}^{2}\sim df\sigma_{X}^{2}\chi^{2}(df)/df.$

In terms of the sampling distribution of (1), then, we have the ratio of two (scaled) $\chi^2$ distributions, one with $df_e = N - 2$ degrees of freedom, and one with $df = N - 1$ degrees of freedom. Or something like:

$\hat{\sigma}_{\hat{\beta_{1}}}^{2}\sim\frac{\sigma_{y}^{2}(1-\rho^{2})\chi^{2}(df_{e})/df_{e}}{df\sigma_{X}^{2}\chi^{2}(df)/df}=\frac{\sigma_{y}^{2}(1-\rho^{2})}{df\sigma_{X}^{2}}\frac{\chi^{2}(df_{e})/df_{e}}{\chi^{2}(df)/df}=\frac{\sigma_{y}^{2}(1-\rho^{2})F(df_{e,}df)}{df\sigma_{X}^{2}},$

which means that the sampling distribution of MOE is:

(2) $\hat{MOE}\sim t_{.975}(N-2)\sqrt{\frac{\sigma_{y}^{2}(1-\rho^{2})F(N-2,N-1)}{(N-1)\sigma_{X}^{2}}}.$

This last equation, that is (2), can be used to obtain quantiles of the sampling distribution of MOE, which enables us to determine assurance MOE, that is the value of MOE that under repeated sampling will not exceed a target value with a given probability. For instance, if we want to know the .80 quantile of estimates of MOE, that is, assurance is .80, we determine the .80 quantile of the (central) F-distribution with N – 2 and N – 1 degrees of freedom and fill in (2) to obtain a value of MOE that will not be exceeded in 80% of replication experiments.

For instance, suppose $\sigma^2_Y = 1$ , $\sigma^2_X = 1$ , $\rho = .50$ , $N = 100$ , and assurance is .80, then according to (2), 80% of estimated MOEs will not exceed the value given by:

vary = 1
varx = 1
rho = .5
N = 100 
dfe = N - 2
dfx - N - 1
assu = .80
t = qt(.975, dfe)
MOE.80 = t*sqrt(vary*(1 - rho^2)*qf(.80, dfe, dfx)/(dfx*varx))
MOE.80

## [1] 0.1880535

What does a quick simulation study tell us?

A quick simulation study may be used to check whether this is at all accurate. And, yes, the estimated quantile from the simulation study is pretty close to what we would expect based on (2). If you run the code below, the estimate equals 0.1878628.

library(MASS)
set.seed(355)
m = c(0, 0)

# note: s below is the variance-covariance matrix. In this case,
# rho and the cov(y, x) have the same values
# otherwise: rho = cov(x, y)/sqrt(varY*VarX) (to be used in the 
# functions that calculate MOE)
# equivalently, cov(x, y) = rho*sqrt(varY*varX) (to be used
# in the specification of the variance-covariance matrix for 
#generating bivariate normal variates)

s = matrix(c(1, .5, .5, 1), 2, 2)
se <- rep(10000, 0)
for (i in 1:10000) {
theData <- mvrnorm(100, m, s)
mod <- lm(theData[,1] ~ theData[,2])
se[i] <- summary(mod)$coefficients[4]
}
MOE = qt(.975, 98)*se
quantile(MOE, .80)

##       80% 
## 0.1878628

Planning for precision

If we want to plan for precision we can do the following. We start by making a function that calculates the assurance quantile of the sampling distribution of MOE described in (2). Then we formulate a squared cost function, which we will optimize for the sample sizeusing the optimize function in R.

Suppose we want to plan for a target MOE of .10 with 80% assurance.We may do the following.

vary = 1
varx = 1
rho = .5
assu = .80
tMOE = .10

MOE.assu = function(n, vary, varx, rho, assu) {
        varY.X = vary*(1 - rho^2)
        dfe = n - 2
        dfx = n - 1
        t = qt(.975, dfe)
        q.assu = qf(assu, dfe, dfx)
        MOE = t*sqrt(varY.X*q.assu/(dfx * varx))
        return(MOE)
}

cost = function(x, tMOE) { 
cost = (MOE.assu(x, vary=vary, varx=varx, rho=rho, assu=assu) 
- tMOE)^2
}

#note samplesize is at least 40, at most 5000. 
#note that since we already know that N = 100 is not enough
#in stead of 40 we might just as well set N = 100 at the lower
#limit of the interval
(samplesize = ceiling(optimize(cost, interval=c(40, 5000), 
tMOE = tMOE)$minimum))

## [1] 321

#check the result: 
MOE.assu(samplesize, vary, varx, rho, assu)

## [1] 0.09984381

Let’s simulate with the proposed sample size

Let’s check it with a simulation study. The value of estimated .80 of estimates of MOE is 0.1007269 (if you run the below code with random seed 335), which is pretty close to what we would expect based on (2).

set.seed(355)
m = c(0, 0)

# note: s below is the variance-covariance matrix. In this case,
# rho and the cov(y, x) have the same values
# otherwise: rho = cov(x, y)/sqrt(varY*VarX) (to be used in the 
# functions that calculate MOE)
# equivalently, cov(x, y) = rho*sqrt(varY*varX) (to be used
# in the specification of the variance-covariance matrix for 
# generating bivariate normal variates)

s = matrix(c(1, .5, .5, 1), 2, 2)
se <- rep(10000, 0)
samplesize = 321
for (i in 1:10000) {
theData <- mvrnorm(samplesize, m, s)
mod <- lm(theData[,1] ~ theData[,2])
se[i] <- summary(mod)$coefficients[4]
}
MOE = qt(.975, 98)*se
quantile(MOE, .80)

##       80% 
## 0.1007269

References

Cumming, G. (2012). Understanding the New Statistics. Effect Sizes, Confidence Intervals, and Meta-Analysis. New York: Routledge
Cumming, G., & Calin-Jageman, R. (2017). Introduction to the New Statistics: Estimation, Open Science, and Beyond. New York: Routledge.
Wilcox, R. (2017). Understanding and Applying Basic Statistical Methods using R. Hoboken, New Jersey: John Wiley and Sons.

July 25, 2017November 7, 2019

Planning for a precise interaction contrast estimate

In my previous post (here), I wrote about obtaining a confidence interval for the estimate of an interaction contrast. I demonstrated, for a simple two-way independent factorial design, how to obtain a confidence interval by making use of the information in an ANOVA source table and estimates of the marginal means and how a custom contrast estimate can be obtained with SPSS.

One of the results of the analysis in the previous post was that the 95% confidence interval for the interaction was very wide. The estimate was .77, 95% CI [0.04, 1.49]. Suppose that it is theoretically or practically important to know the value of the contrast to a more precise degree. (I.e. some researchers will be content that the CI allows for a directional qualitative interpretation: there seems to exist a positive interaction effect, but others, more interested in the quantitative questions may not be so easily satisfied). Let’s see how we can plan the research to obtain a more precise estimate. In other words, let’s plan for precision.

Of course, there are several ways in which the precision of the estimate can be increased. For instance, by using measurement procedures that are designed to obtain reliable data, we could change the experimental design, for example switching to a repeated measures (crossed) design, and/or increase the number of observations. An example of the latter would be to increase the number of participants and/or the number of observations per participant. We will only consider the option of increasing the number of participants, and keep the independent factorial design, although in reality we would of course also strive for a measurement instrument that generally gives us highly reliable data. (By the way, it is possible to use my Precision application to investigate the effects of changing the experimental design on the expected precision of contrast estimates in studies with 1 fixed factor and 2 random factors).

The plan for the rest of this post is as follows. We will focus on getting a short confidence interval for our interaction estimate, and we will do that by considering the half-width of the interval, the Margin of Error (MOE). First we will try to find a sample size that gives us an expected MOE (in repeated replication of the experiment with new random samples) no more than a target MOE. Second, we will try to find a sample size that gives a MOE smaller than or equal to our target MOE in a specifiable percentage (say, 80% or 90%) of replication experiments. The latter approach is called planning with assurance.

Let us get back to some of the SPSS output we considered in the previous post to get the ingredients we need for sample size planning. First, the ANOVA table.

Table 1. ANOVA source table

We are interested in estimating and optimizing the precision of an interaction contrast estimate. The first things we need are an expression of the error variance needed to calculate the standard error of the estimate and the degrees of freedom that were used in estimating the error variance. In general, the error variance needed is the same error variance you would use in performing an F-test for the specific effect, in this case the interaction effect.

Thus, we note the error variance used to test the interaction effect, i.e. mean square error, and the degrees of freedom. The value of mean square error is 3.324, and the degrees of freedom are 389. Note that this value is the total sample sizes minus the number of conditions (393 – 4 = 389), or, equivalently, the total sample sizes minus the degrees of freedom of the intercept, the main effects, and the interaction (393 – (1 + 1 + 1 + 1) = 389). I will call these degrees of freedom the error degrees of freedom, df_e.

MOE can be obtained by multiplying a critical t-value with the same degrees of freedom as the error degrees of freedom with the standard error of the estimate.

The standard error of the contrast estimate is

$\hat{\sigma_\psi}= \sqrt{\sum{c_i^2MS_e/n_i}},$

where $c_i$ is the contrast weight for the i-th condition mean, and $n_i$ the number of observations (in our example participants) in treatment condition i. Note that $MS_e / n_i$ is the variance of treatment mean i, the square root of which gives the familiar standard error of the mean.

The contrast weights we used to estimate the 2 x 2 interaction were {-1, 1, 1, -1}. So, the expression for MOE becomes

$MOE = t_{.975}(df_e)\sqrt{\sum{c_i^2MS_e/n_i}}=t_{.975}(df_e)\sqrt{4MS_e/n_i} = 2t_{.975}(df_e)\sqrt{MS_e/n_i}.$

Thus, suppose we have the independent 2×2 factorial design, $n_i = 100$ , and the true value of Mean Square Error is 3.324, then MOE for the contrast estimate equals

$MOE = 2*t_{.975}(396)*\sqrt{3.324/100} = 0.7071$

.
Note that this is the value of MOE we obtain on average in repeated replications with new samples, if we use sample sizes of 100 (total number of participants is 400) and if the true value of the error variance is 3.324. The value is close to the value we obtained in the previous post (MOE = 0.72) because the sample sizes were very close to 100 per group.

Now, we found the original confidence interval too wide, and we have just seen how 100 participants per group does not really help. MOE is only slightly smaller than our originally obtained MOE. We need to set a target MOE and then figure out how many participants we need to get that target MOE.

Intermezzo: Rules of thumb for target MOE

(Here are some updated rules of thumb: https://the-small-s-scientist.blogspot.com/2018/11/contrast-tutorial.html)

In the absence of theoretical or practical considerations about the precision we want, we may want to use rules of thumb. My (very first proposal for) rules of thumb are based on the default interpretations of Cohen’s d. Considering the absolute values of d ≤ .10 to be negligible d = .20 small, d = .50 medium and d = .80 large. (I really do not like rules-of-thumb, because using them is a sign that you are not thinking).

Now, suppose that we interpret the confidence interval as a range of plausible values for the true value of the effect size. It is not at all clear to me what such a supposition entails, but let’s simply take it for granted right now (please don’t). Then, I think it is reasonable to say that being able to distinguish between small and negligible effects sizes is relatively precise. Thus a MOE of .05 (pooled) standard deviations can be considered precise because (on average) the 95% CI for the small effect sizes is [.15, .25], assuming we know the value of the standard deviation, so negligible effects will not be deemed plausible values on average, since effect sizes smaller than .10 are outside the interval.

By essentially the same reasoning. if we cannot distinguish between large and negligible effects, we are not estimating things very precisely. Therefore, a MOE of .80 standard deviations can be considered to be not very precise. On average, the CI for an existing large effect, will be [0, 1.60], so it includes both negligible and very large effects as plausible values.

For medium (does it make sense to speak of medium precision?) precision I would like to suggest .20-.25 standard deviations. On average, with this value for MOE, if there is a medium effect, small effects and large effects are relatively implausible. In the case of small effects, medium precision entails that on average both effects in the opposite direction and medium effects are among the plausible values.

Of course, I am interpreting the d-values as strict boundaries, but the scale is not categorical, but continuous. So instead of small, large effect sizes, it’s better to speak of smallish and largish effect sizes. And as soon as I find a variant for medium effects sizes I will also include that term in the list.

Note: sample size planning may indicate that precision of MOE = .20-.25 standard deviations is unattainable. In that case, we will simply have to accept that our precision does not lead to confident conclusions about the population effect size. (Once I showed one of my colleagues my precision app, during which he said: “that amount of precision requires a very large sample. I do not like your ideas about sample size planning”).

(By the way, I am also considering rules-of-thumb for target MOE that include assurance. Something like: high precision is when repeated experiments have a high probability of distinguishing small and negligible effects; in that case the average MOE will be smaller than .05).

Planning for precision

Let’s plan for a precision of 0.25 standard deviation. In our case, that standard deviation is the pooled standard deviation: the square root of Mean Square Error. The (estimated) value of Mean Square Error is 3.324 (see Table 1), so our value for the standard deviation is 1.8232. Our target MOE is, therefore, 0.4558.

Let’s make things very clear. Here we are planning for a target MOE based on an estimate of the pooled standard deviation (and on assumptions about the population distribution). In order for our planning to be of practical value, we need some reassurance that that estimate is trustworthy. One way of doing that is to consider the CI for the standard deviation. I will not discuss that topic, and simply give you a CI: [2.90, 3.86].

Take a look at the expression for MOE.

$MOE = 2*t_{.975}(df_e)\sqrt{(MS_w / n_i)},$

where $df_e = 4(n_i - 1)$ , since we are considering the 2×2 design.

Since our target MOE equals .4588, our goal becomes to solve the following equation for $n_i$ , since we want the sample size:

$0.4558 = 2*t_{.975}(4(n_i - 1)\sqrt{(MS_w / n_i)},$

However, because $n_i$ determines both the standard error and the degrees of freedom (and thereby the critical value of t), the equation may be a little hard to solve. So, I will create a function in R that enables me to quite easily get the required sample size. (It is relatively easy to create a more general function (see the Precision App), but here I will give an example tailored to the specific situation at hand).

First we create a function to calculate MOE:

MOE = function(n) {
  MOE = 2*qt(.975, 4*(n - 1))*sqrt(3.324/n)
}

Next, we will define a loss function and use R’s built-in optimize function to determine the sample size. Note that the loss-function calculates the squared difference between MOE based on a sample size n and our target MOE. The optimize function minimizes that squared difference in terms of sample size n (starting with n = 100 and stopping at n = 1000).

loss <- function(n) {
  (MOE(n) - 0.4558)^2
}

optimize(loss, c(100, 1000))

## $minimum
## [1] 246.4563
## 
## $objective
## [1] 8.591375e-18

Thus, according to the optimize function we need 247 participants (per group; total N = 988), to get an expected MOE equal to our target MOE. The expected MOE equals 0.4553, which you can confirm by using the MOE function we made above.

Planning with assurance

Although expected MOE is close to our target MOE, there is a probability 50% that the obtained MOE will be larger than our target MOE. In other words, repeated sampling will lead to obtained MOEs larger than what we want. That is to say, we have 50% assurance that our obtained MOE will be at least as small as our target MOE.

Planning with assurance means that we aim for a certain specified assurance that our obtained MOE will not exceed our target MOE. For instance, we may want to have 80% assurance that our obtained MOE will not exceed our target MOE.

Basically, what we need to do is take the sampling distribution of the estimate of Mean Square Error into account. We use the following formula (see also my post introducing the Precision App for the general formulae: https://the-small-s-scientist.blogspot.nl/2017/04/planning-for-precision.html).

$MOE_{\gamma} = 2*t_{.975}(df)*\sqrt{MS_w/n_i*\chi^2_{\gamma}(df)/df},$

where $gamma$ is the assurance expressed in a probability between 0 and 1.

Let’s do it in R. Again, the function that calculates assurance MOE is tailored for the specific situation, but it is relatively easy to formulate these functions in a generally applicable way,

MOE.gamma = function(n) {
  df = 4*(n-1)
  MOE = 2*qt(.975, df)*sqrt(3.324/n*qchisq(.80, df)/df)
}
loss <- function(n) {
  (MOE.gamma(n) - 0.4558)^2
}

optimize(loss, c(100, 1000))

## $minimum
## [1] 255.576
## 
## $objective
## [1] 2.900716e-18

Thus, according to the results, we need 256 persons per group (N = 1024 in total) to have a 80% probability of obtaining a MOE not larger than our target MOE. In that case, our expected MOE will be 0.4472.

May 3, 2017October 22, 2019

Planning for Precision: simulation results for four designs with four conditions

This is the third post about the Planning for Precision app (in the future I’ll explain the difference between Planning for Precision and Precision for Planning). Some background information about the application can be found here: http://the-small-s-scientist.blogspot.com/2017/04/planning-for-precision.html.

In this post, I want to present the simulation results for 4 designs with 4 conditions. The designs are: the counter balanced design (see previous post), the fully-crossed design, the stimulus-within-condition design, and the stimulus-and-participant-within-condition design (the both-within-condition design). I have not included the participants-within-condition design, because this is simply the mirror-image (so to say) of the stimulus-within-condition design.

In one of my next posts, I will describe some more background information about planning for precision, but some of the basics are as follows. We have a design with 4 treatment conditions, and what we want do is to estimate differences between these condition means by using contrasts. For instance, we may be interested in the (amount of) difference between the first mean, maybe because it is a control-condition with the average of the other three conditions: μ₁ – (μ₂ + μ₃ + μ₄)/3 = 1*μ₁ – 1/3*μ₂ -1/3*μ₃ – 1/3*μ₄. The values {1, -1/3, -1/3, -1/3} are the contrast weights, and for the result we use the term ψ.

The value of ψ is estimated on the basis of estimates of the population means, that is, the sample means or condition means. Due to sampling error, the contrast estimate varies from sample to sample and the amount of sampling error can be expressed by means of a confidence interval. Conceptually, the confidence interval expresses the precision of the estimate: the wider the confidence interval, the less precise the estimate is.

The Margin of Error (MOE) of an estimate is the half-width of the confidence interval, so the confidence interval is the estimate plus or minus MOE. We will take MOE as an expression of the precision of the estimate (the less the value of MOE the more precise the estimate). Now, if you want to estimate an effect size, more precision (lower value of MOE; less wide confidence interval) is better than less precision (higher value of MOE; wider confidence interval). The app let’s you specify the design and the contrast weights and helps you find the minimum required sample sizes (for participants and stimuli) for a given target MOE. (You can also play with the designs to see which design gives you smallest expected MOE).

Crucially, if you plan for precision, you also want to have some assurance that the MOE you are likely to obtain in you actual experiment will not be larger than you target MOE. Compare this with power: 80% power means that the probability that you will reject the null-hypothesis is 80%. Likewise, assurance MOE of 80% means that there is an 80% probability that your obtained MOE will be no larger than assurance MOE.

The simulations (with N = 10000 replications) estimate Expected MOE as well as Assurance MOE for assurances of .80, .90, .95, and .99, for 4 designs with 4 treatment conditions, with a total number of 48 participants and 24 stimuli (items). The MOEs are given for three standard constrasts: 1) the difference between the first mean and the mean of the other three, with weights {1, -1/3, -1/3, -1/3}; 2) the difference between the second mean and the mean of conditions three and four, with weights {0, 1, -1/2, -1/2}; 3) the difference between the third and fourth condition means, with weights {0, 0, 1, -1}.

I will present the results in separate tables for the 4 designs considered and include percentage difference between expected values of assurance MOE and the estimated values estimated values.

The fully crossed design

The results are in the following table.

The percentage difference between the expected quantiles (= assurance MOEs for given insurance; i.e. q.80 is expected or estimated 80% Assurance MOE) and the estimated quantiles are: .80: 0.11%; .90: 0.05%; .95: -0.14%; 99: -0.05%.

The counter balanced design

The results are presented in the following table.

The percentage difference between the expected quantiles and the estimated quantiles are: .80: 0.03%; .90: 0.13%; .95: 0.09%, .99: -0.23%.

The stimulus-within-condition design

The following table contains the details.

The percentage difference between the expected quantiles and the estimated quantiles are: .80: -0.11%; .90: -0.33%; .95: -0.55%, .99: -0.70%.

Both-participant-and-stimulus-within-condition design

Here is the table.

And the percentage differences are: .80: -0.34%; .90: -0.59%; .95: -0.82%; .99: -1.06%.

Conclusion

The results show that the simulation results are quite consistent with the expected values based on mixed model ANOVA. We can see that the differences between expected and estimated values increase the less the number of participants and items per condition. For instance, in the both within condition design 12 participants respond to 6 stimuli in one of the four treatment conditions. The fact that even with these small samples sizes the results seem to agree to an acceptable degree is (to my mind) encouraging. Note that with small samples the expected assurance MOES are slightly lower than the estimates, but the largest difference is -1.06% (see the MOE for 99% assurance).

May 1, 2017October 22, 2019

Planning for Precision: first simulation results

In this post, I want to share the results of the first simulation study to “test” my Planning for Precision app. More details about the app can be found in a previous post: here.

I have included the basic logic of the simulations (including R code) in a document that you can download: https://drive.google.com/open?id=0B4k88F8PMfAhSlNteldYRWFrQTg.

The simulation study simulates responses from a four condition counter balanced design, with p = 48 participants and q = 24 stimuli/items. Here, we will focus on expected and assurance MOE for three contrasts. The first contrast estimates the difference between the first mean and the average of the other three, the second contrast the difference between the second mean and the average of the third and fourth means, and the final contrast the difference between the means of the third and fourth contrasts.

Expected MOE is compared to the mean of the estimated MOE for each of the contrasts (based on 10000 replications). Assurance MOE is judged for assurance of .80, .90, .95 and .99, by comparing the calculations in the app with the corresponding quantile estimates of the simulated distributions.

Results

Note that in the above table, the Expected Mean MOE is what I have called Expected MOE, and the q.80 through q.99 are quantiles of the distribution of MOE. As an example, q.80 is the quantile corresponding to assurance MOE with 80% assurance, Expected q.80 is the value of assurance MOE calculated with the theoretical approach, and Estimated q.80 is the estimated quantile based on the simulation studies.

Importantly, we can see that most of the figures agree to a satisfying degree. If we look at the relative differences, expressed in percentages for the assurance MOEs, we get 0.0325% for q.80, 0.1260% for q.90, 0.0933% for q.95, and -0.2324% for q.99.

Conclusion

The first simulation results seem promising. But I still have a lot of work to do for the rest of the designs.

April 29, 2017June 9, 2021

Planning for precision with samples of participants and items

Many experiments involve the (quasi-)random selection of both participants and items. Westfall et al. (2014) provide a Shiny-app for power-calculations for five different experimental designs with selections of participants and items. Here I want to present my own Shiny-app for planning for precision of contrast estimates (for the comparison of up to four groups) in these experimental designs. The app can be found here: https://gmulder.shinyapps.io/precision/

(Note: I have taken the code of Westfall’s app and added code or modified existing code to get precision estimates in stead of power; so, without Westfall’s app, my own modified version would never have existed).

The plan for this post is as follows. I will present the general theoretical background (mixed model ANOVA combined with ideas from Generalizability Theory) by considering comparing three groups in a counter balanced design.
Note 1: This post uses mathjax, so it’s probably unreadable on mobile devices. Note: a (tidied up) version (pdf) of this post can be downloaded here: download the pdf
Note 2: For simulation studies testing the procedure go here: https://the-small-s-scientist.blogspot.nl/2017/05/planning-for-precision-simulation.html
Note 3: I use the terms stimulus and item interchangeably; have to correct this to make things more readable and comparable to Westfall et al. (2014).
Note 4: If you do not like the technical details you can skip to an illustration of the app at the end of the post.

The general idea

The focus of planning for precision is to try to minimize the half-width of a 95%-confidence interval for a comparison of means (in our case). Following Cumming’s (2012) terminology I will call this half-width the Margin of Error (MOE). The actual purpose of the app is to find required sample sizes for participants and items that have a high probability (‘assurance’) of obtaining a MOE of some pre-specified value.

Expected MOE for a contrast

For a contrast estimate $\hat{\psi}$ we have the following expression for the expected MOE.

$E(MOE) = t_{.975}(df)*\sigma_{\hat{\psi}},$

where $\sigma_{\hat{\psi}}$ is the standard error of the contrast estimate. Of course, both the standard error and the df are functions of the sample sizes.

For the standard error of a contrast with contrast weights $c_i$ through $c_a$ , where a is the number of treatment conditions, we use the following general expression.

$\sigma_{\hat{\psi}} = \sqrt{\sum c^2_i \frac{\sigma^2_w}{n}},$

where n is the per treatment sample size (i.e. the number of participants per treatment condition times the number of items per treatment condition) and $\sigma^2_w$ the within treatment variance (we assume homogeneity of variance).

For a simple example take an independent samples design with n = 20 participants responding to 1 item in one of two possible treatment conditions (this is basically the set up for the independent t-test). Suppose we have contrast weights $c_1 = 1$ and $c_2 = -1$ , and $\sigma^2_w = 20$ , the standard error for this contrast equals $\sigma_{\hat{\psi}} = \sqrt{\sum c^2_i\frac{\sigma^2_w}{n}} = \sqrt{2*20/20} = \sqrt{2}$ . (Note that this is simply the standard error of the difference between two means as used in the independent samples t-test).

In this simple example, df is the total sample size (N = n*a) minus the number of treatment conditions (a), thus $df = N - a = 38$ . The expected MOE for this design is therefore, $E(MOE) = t_{.975}(38)*\sqrt{2} = 2.0244*1.4142 = 2.8629$ . Note that using these figures entails that 95% of the contrast estimates will take values between the true contrast value plus and minus the expected MOE: $\psi \pm 2.8629$ .

For the three groups case, and contrast weights { $1, -1/2, -1/2$ }, the same sample sizes and within treatment variance gives $E(MOE) = t_{.975}(57)*\sqrt{1.5*\frac{20}{20}} = 2.4525$ .

(If you like, I’ve written a little document with derivation of the variance of selected contrast estimates in the fully crossed design for the comparison of two and three group means. That document can be found here: https://drive.google.com/open?id=0B4k88F8PMfAhaEw2blBveE96VlU)

The focus of planning for precision is to try to find sample sizes that minimize expected MOE to a certain target MOE. The app uses an optimization function that minimizes the squared difference between expected MOE and target MOE to find the optimal (minimal) sample sizes required.

Planning with assurance

If the expected MOE is equal to target MOE, the sample estimate of MOE will be larger than your target MOE in 50% of replication experiments. This is why we plan with assurance (terminology from Cumming, 2012). For instance, we may want to have a 95% probability (95% assurance) that the estimated MOE will not exceed our target MOE.

In order to plan with assurance, we need (an approximation of) the sampling distribution of MOE. In the ANOVA approach that underlies the app, this boils down to the distribution of estimates of $\sigma^2_w$ :

$MS_w \sim \sigma^2_w*\chi^2(df)/df,$

thus

$\hat{MOE} \sim t_{.975}(df)\sqrt{\frac{1}{n}\sum{c_i^2}\sigma^2_w*\chi^2(df)/df}.$

In terms of the two-groups independent samples design above: the expected MOE equals 2.8629. But, with df = 38, there is an 80% probability (assurance) that the estimated MOE will be no larger than:

$\hat{MOE}_{.80} = 2.0244 * \sqrt{1/20*2*20*45.07628/38} = 3.1181.$

Note that the 45.07628 is the quantile $q_{.80}$ in the chi-squared (df = 38) distribution. That is $P(\chi^2(38) \leq 45.07628) = .80$ .

The app let’s you specify a target MOE and a value for the desired assurance ( $\gamma$ ) and will find the combination of number of participants and items that will give an estimated MOE no larger than target MOE in $\gamma$ % of the replication experiments.

The mixed model ANOVA approach

Basically, what we need to plan for precision is to able to specify $\sigma^2_w$ and the degrees of freedom. We will specify $\sigma^2_w$ as a function of variance components and use the Satterthwaite procedure to approximate the degrees of freedom by means of a linear combination of expected mean squares. I will illustrate the approach with a three-treatment conditions counterbalanced design.

A description of the design

Suppose we are interested in estimating the differences between three group means. We formulate two contrasts: one contrast estimates the mean difference between the first group and the average of the means of the second and third groups. The weights of the contrasts are respectively {1, -1/2, -1/2}, and {0, 1, -1}.

We are planning to use a counterbalanced design with a number of participants equal to p and a sample of items of size q. In the design we randomly assign participants to a groups, where a is the number of conditions, and randomly assign items to a lists (see Westfall et al., 2014 for more details about this design). All the groups are exposed to all lists of stimuli, but the groups are exposed to different lists in each condition. The number of group by list combinations equals $a^2$ , and the number of observations in each group by list combination equals $\frac{1}{a^2}pq$ . The condition means are estimated by combining a group by list combinations each of which composed of different participants and stimuli. The total number of observations per condition is therefore, $\frac{a}{a^2}pq = \frac{1}{a}pq$ .

The ANOVA model

The ANOVA model for this design is

$Y_{ijk} = \mu + \alpha_i + \beta_j + \gamma_k + (\alpha\beta)_{ij} + (\alpha\gamma)_{ik} + e_{ijk},$

where the effect $\alpha_i$ is a constant treatment effect (it’s a fixed effect), and the other effect are random effects with zero mean and variances $\sigma^2_\beta$ (participants), $\sigma^2_\gamma$ (items), $\sigma^2_{\alpha\beta}$ (person by treatment interaction), $\sigma^2_{\alpha\gamma}$ (item by treatment interaction) and $\sigma^2_e$ (error variance confounded with the person by item interaction). Note: in Table 1 below, $\sigma^2_e$ is (for technical reasons not important for this blogpost) presented as this confounding $[\sigma^2_{\beta\gamma} + \sigma^2_e]$ .

We make use of the following restrictions (Sahai & Ageel, 2000): $\sum_{i = 1}^a = 0$ , and $\sum_{i=1}^a(\alpha\beta)_{ij} = \sum_{i=1}^a(\alpha\gamma)_{ik} = 0$ . The latter two restrictions make the interaction-effects correlated across conditions (i,e. the effects of person and treatment are correlated across condition for the same person, likewise the interaction effects of item and treatment are correlated across conditons for the same item. Interaction effects of different participants and items are uncorrelated). The covariances between the random effects $\beta_j, \gamma_i, (\alpha\beta)_{ij}, (\alpha\gamma)_{ik}, e_{ijk}$ are assumed to be zero.

Under this model (and restrictions) $E((\alpha\beta)^2) = \frac{a - 1}{a}\sigma^2_{\alpha\beta}$ , and $E((\alpha\gamma)^2) = \frac{a - 1}{a}\sigma^2_{\alpha\gamma}$ . Furthermore, the covariance of the interactions between treatment and participant or between treatment and item for the same participant or item are $-\frac{1}{a}\sigma^2_{\alpha\beta}$ for participants and $-\frac{1}{a}\sigma^2_{\alpha\gamma}$ for items.

Within treatment variance

In order to obtain an expectation for MOE, we take the expected mean squares to get an expression or the expected within treatment variance $\sigma^2_w$ . These expected means squares are presented in Table 1.

The expected within treatment variance can be found in the Treatment row in Table 1. It is comprised of all the components to the right of the component associated with the treatment effect ( $\theta^2_a$ ). Thus, $\sigma^2_w = \frac{q}{a}\sigma^2_{\alpha\beta} + \frac{p}{a}\sigma^2_{\alpha\gamma}+[\sigma^2_{\beta\gamma} + \sigma^2_e]$ . Note that the latter equals the sum of the expected mean squares of the Treatment by Participant ( $E(MS_{tp})$ ) and the Treatment by Item ( $E(MS_{ti})$ ) interactions, minus the expected mean square associated with Error ( $E(MS_e)$ ).

Degrees of freedom

The second ingredient we need in order to obtain expected MOE are the degrees of freedom that are used to estimate the within treatment variance. In the ANOVA approach the within treatment variance is estimated by a linear combination of mean squares (as described in the last sentence of the previous section. This linear combination is also used to obtain approximate degrees of freedom using the Satterthwaite procedure:

$df =\frac{(E(MS_{tp}) + E(MS_{ti}) - E(MS_e))^2}{\frac{E(MS_{tp})^2}{(a - 1)(p-a)}+\frac{E(MS_{ti})^2}{(a - 1)(q-a)}+\frac{E(MS_e)^2}{(p-a)(q-a)}}$

Expected MOE

(Note: I can’t seem to get mathjax to generate align environments or equation arrays, so the following is ugly; Note to self: next time use R-studio or Lyx to generate R-html or an equivalent format).

The expected value of MOE for the contrasts in the counter balanced design is:

$E(MOE) = t(df)*\sqrt{(\sum_{i=1}^a c^2_i)(\frac{1}{a}pq)^{-1}\sigma^2_w}$

$= t(df)*\sqrt{(\sum_{i=1}^a c^2_i)(\frac{1}{a}pq)^{-1}(\frac{q}{a}\sigma^2_{\alpha\beta} + \frac{p}{a}\sigma^2_{\alpha\gamma}+[\sigma^2_{\beta\gamma} + \sigma^2_e])}$

$=t(df)*\sqrt{(\sum_{i=1}^a c^2_i)(pq)^{-1}(q\sigma^2_{\alpha\beta} + p\sigma^2_{\alpha\gamma}+a[\sigma^2_{\beta\gamma} + \sigma^2_e])}$

$=t(df)*\sqrt{(\sum_{i=1}^a c^2_i)(\sigma^2_{\alpha\beta}/p + \sigma^2_{\alpha\gamma}/q +a[\sigma^2_{\beta\gamma} + \sigma^2_e]/pq)}$

Finally an example

Suppose we the scores in three conditions are normally distributed with (total) variances $\sigma^2_1 = \sigma^2_2 = \sigma^2_3 = 1.0$ . Suppose furthermore, that 10% of the variance can be attributed to treatment by participant interaction, 10% of the variance to the treatment by item interaction and 40% of the variance to the error confounded with the participant by item interaction. (which leaves 40% of the total variance attributable to participant and item variance.

Thus, we have $\sigma^2_{tp} = E((\alpha\beta)^2) = .10$ , $\sigma^2_{ti} = E((\alpha\gamma)^2) = .10$ , and $\sigma^2_e = .40$ . Our target MOE is .25, and we plan to use the counterbalanced design with p = 30 participants, and q = 15 items (stimuli).

Due to the model restrictions presented above we have $\sigma^2_{\alpha\beta} = \frac{a}{a - 1}\sigma^2_{tp} = \frac{3}{2}*.10 = .15$ , $\sigma^2_{\alpha\gamma} = .15$ , and $\sigma^2_e = .40$ .

The value of $\sigma^2_w$ is therefore, $5*.15 + 10*.15 +.40 = 2.65$ , and the approximate df equal $df = (2.65^2) / ((5*.15 + .40)^2/(2*27) + (10*.15+.40)^2/(2*12) + .40^2/(27*12)) = 74.5874$ .

For the first contrast, with weights {1, -1/2. -1/2}, then, the Expected value for the Margin of Error is $E(MOE) = t_{.975}(74.5874)*\sqrt{(1.5 * (.15/30 + .15/15 + 3*.40/(30*15))} = 0.3243$ .

For the second contrast, with weights {0, 1, -1}, the Expected value of the Margin of Error is $t_{.975}(74.5874)*\sqrt{(2*(.15/30 + .15/15 + 3*.40/(30*15))} = 0.3745$

Thus, using p = 30 participants, and q = 15 items (stimuli) will not lead to an expected MOE larger than the target MOE of .25.

We can use the app to find the required number of participants and items for a given target MOE. If the number of groups is larger than two, the app uses the contrast estimate with the largest expected MOE to calculate the sample sizes (in the default setting the one comparing only two group means). The reasoning is that if the least precise estimate (in terms of MOE) meets our target precision, the other ones meet our target precision as well.

Using the app

I’ve included lot’ of comments in the app itself, but please ignore references to a manual (does not exist, yet, except in Dutch) or an article (no idea whether or not I’ll be able to finish the write-up anytime soon). I hope the app is pretty straightforward. Just take a look at https://gmulder.shinyapps.io/precision/, but the basic idea is:
– Choose one of five designs
– Supply the number of treatment conditions
– Specify contrast(weights) (or use the default ones)
– Supply target MOE and assurance
– Supply values of variance components (read (e,g,) Westfall, et al, 2014, for more details).
– Supply a number of participants and items
– Choose run precision analysis with current values or
– Choose get sample sizes. (The app gives two solutions: one minimizes the number of participants and the other minimizes the number of stimuli/items). NOTE: the number of stimuli is always greater than or equal to 10 and the number of participants is always greater than or equal to 20.

An illustration

Take the example above. Out target MOE equals .25, and we want insurance of .80 to get an estimated MOE of no larger than .25. We use a counter-balanced design with three conditions, and want to estimate two contrasts: one comparing the first mean with the average of means two and three, and the other contrast compares the second mean with the third mean. We can use the default contrasts.

For the variance components, we use the default values provided by Westfall et al. (2014) for the variance components. These are also the default values in the app (so we don’t need to change anything now).

Let’s see what happens when we propose to use p = 30 participants and q = 15 items/stimuli.

Here is part of a screenshot from the app:

These results show that the expected MOE for the first contrast (comparing the first mean with the average of the other means) equals 0.3290, and assurance MOE for the same contrasts equals 0.3576. Remember that we specified the assurance as .80. So, this means that 80% of the replication experiments give estimated MOE as large as or smaller than 0.3576. But we want that to be at most 0.2500. Thus, 30 participants and 15 items do suffice for our purposes.

Let’s use to app to get sample sizes. The results are as follows.

The app promises that using 25 stimuli combined with 290 participants or 25 participants and 290 items will do the trick (the symmetry of these results are due to the fact that the interaction components are equal; both the treatment by participant and the treatment by stimulus interaction component equal .10). Since we have 3 treatment conditions using 290 participants or stimuli is a little awkward, so I suggest to use 291 (equals 97 participants per group or 97 items per list). (300 is a much nicer figure of course). Likewise, as it is hard to equally divide 25 stimuli or participants over three lists or groups, use a multiple of three (say: 27).

If we input the suggest sample sizes in the app, we see the following results if we choose the run precision analysis with current values.

As you can see: Assurance MOE is close to 0.25 (.24) for the second contrast (the least precise one), so 80% of replication experiments will get estimated MOE of 0.25 (.24) or smaller. The expected precision is 0.22. The first contrast (which can be estimated with more precision) has assurance MOE of 0.21 and expected MOE of approximately 0.19. Thus, the sample sizes lead to the results we want.

References

Cumming, G. (2012). Understanding the New Statistics. New York/London: Routledge.

Sahai, H., & Ageel, M. I. (2000). The analysis of variance. Fixed, Random, and Mixed Models. Boston/Basel/Berlin: Birkhäuser.

Westfall, J., Kenny, D. A., & Judd, C. M. (2014). Statistical power and optimal design in experiments in which samples of participants respond to samples of stimuli. Journal of Experimental Psychology: General, 143(5), 2020-2045.