December 2017 - The small S scientist

In a previous post (here), we saw how we can determine sample size for obtaining, with assurance, a precise interaction contrast estimate. In that post we considered a 2 x 2 factorial design. In this post, I will extend the discussion to the mixed model case. That is, we will consider sample size planning for a precise interaction estimate in case of a design with 2 fixed factors and two random factors: participant and stimulus (item). (A pdf version of this post can be found here: view pdf. )

In order to keep things relatively simple, we will focus on a design where both participants and items are nested under condition. So, each treatment condition has a unique sample of participants and items. We will call this design the both-within-condition design (see, for instance, Westfall et al. 2014, for detailed descriptions of this design). We will analyse the 2 x 2 factorial design as a single factor design (the factor has a = 4 levels) and formulate an interaction contrast.

Let’s start with p participants and q stimuli. We randomly assign n= p/a participants and m = q/a stimuli to each of the a treatment levels. The ANOVA table for the design is presented in Table 1.

Expected Mean Squares Both Within Condition Design

We will use the ANOVA table to illustrate a few concepts that are important to consider when analysing data using mixed modeling. Maybe you remember that in the previous post, we used the ANOVA source table to obtain an expression for the variance of a contrast. In particular, we used the error variance (MSerror) that is also used to form the F-ratio for testing the interaction effect.

Obtaining an apropriate error term

Now, the inclusion of the second random factor (i.e. stimulus in addition to participant) leads, in comparison to the design in the previous post, to a complication. In order to see this, take a look again at the ANOVA table we get when we use SPSS univariate (see Figure 1 and SPSS syntax below). (Important: do not use SPSS GLM Univariate for estimating contrasts in this design; the procedure uses the incorrect standard error; I am using the procedure now just for illustrating a few key concepts).

UNIANOVA score BY cond pp ss   
/RANDOM=pp ss   
/METHOD=SSTYPE(3)   
/INTERCEPT=INCLUDE   
/CRITERIA=ALPHA(0.05)   
/DESIGN=cond pp WITHIN cond ss WITHIN cond 
/CONTRAST(cond) = SPECIAL(1, -1, -1, 1).

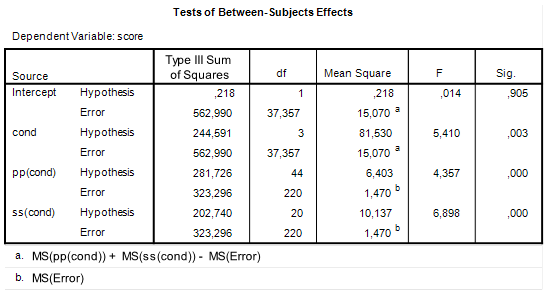Figure 1: SPSS GLM ANOVA output

We can see that the effect of condition is not tested against MSError but against an errorterm formed by linearily combining MSpp, MSss, and MSerror. In particular, MSpp and MSss are added and MSerror is subtracted. See footnote a below the source table. It’s a bit hard to explain why that is done, but I’ll have a go at an explanation nonetheless.

Take a look at Table 1 and focus on the Participant row. The expected Mean Square (EMS) associated with Participant is $m\sigma^2_p + \sigma^2_e$ . Now, suppose that due to some freak accident of nature there are no differences in the mean scores (averaged of stimuli) of each participant. In that case, $\sigma^2_p = 0$ . This means that under these circumstances the expected mean square associated with participants is simply an estimate of the error variance with $p - a$ degrees of freedom, because $m\sigma^2_p + \sigma^2_e = m*0 + \sigma^2_e = \sigma^2_e$ , if $\sigma^2_p = 0$ . Of course, the other estimate of the Error variance is MSError and this estimate is based on $a(n - 1)(m - 1)$ degrees of freedom. The logic of the F-test is that under the null-hypothesis, in our case that $\sigma^2_p = 0$ , the ratio of these two estimates of the error variance follows an F-distribution with $p - a$ and $a(n - 1)(m - 1)$ degrees of freedom.

Now focus on the Treatment row in Table 1. The expected mean square associated with Treatment equals $nm\theta^2_T + m\sigma^2_p + n\sigma^2_s + \sigma^2_e$ . If we now suppose that there is no difference between the treatment means, that is $\theta^2_T = 0$ , MSTreatment does not estimate $\sigma^2_e$ , but $m\sigma^2_p + n\sigma^2_s + \sigma^2_e$ . Note that no other source of variance has an expected mean square that is equal to the latter figure. That is, in contrast to our test of the Participant factor, where under the null-hypotheses two Mean Squares estimate the error variance, i.e. MSParticipant and MSError, no mean square is available to form an F-ratio to test the Treatment effect.

But a linear combination of MSParticipant, MSStimulus and MSError, does provide an estimate with expected value $m\sigma^2_p + n\sigma^2_s + \sigma^2_e$ . Namely, the sum of the participant and stimulus mean squares minus mean square error: $[m\sigma^2_p + \sigma^2_e] + [m\sigma^2_s + \sigma^2_e] - [\sigma^2_e] = m\sigma^2_p + n\sigma^2_s + \sigma^2_e$ . It is exactly this linear combination of mean squares that is used in the F-ratio to obtain an error term against which to test the Treatment effect in Figure 1: $6.403 + 10.137 - 1.470 = 15.070$ . We will also use this figure to obtain the variance (and standard error) of our contrast estimate.

Degrees of freedom

If you take a closer look at Figure 1, in particular the degrees of freedom column, you will notice that the degrees of freedom associated with the error term that is used to test the Treatment effect is a fractional number and not a nice round number that you would expect to get if you only consider the degrees of freedom in Table 1. The cause of this fractional number is that we cannot simply use the degrees of freedom of the mean square used to test the treatment effect, because that mean square does not exist. Indeed, we had to combine three mean squares in order to obtain an estimate of the error term for the Treatment effect. The consequence of this is that we will have to use an approximation of the degrees of freedom associated with that error term.

SPSS (and my precision app) use the Satterthwaite procedure to approximate the degrees of freedom of the error term. That approximation is as follows (notice that the numerator is equal to the linear combination of mean squares used to obtain the error term).

$df=\frac{(MSp+MSs-MSe)^{2}}{\frac{MSp^{2}}{df_{p}}+\frac{MSs^{2}}{df_{s}}+\frac{MSe^{2}}{df_{e}}}.$

Thus, using the results in Figure 1.

MSp = 6.403
MSs = 10.137
MSe = 1.470
dfp = 44
dfs = 20
dfe = 220
df = (MSp + MSs - MSe)^2 / (MSp^2/dfp + MSs^2/dfs + MSe^2/dfe)
df

## [1] 37.35559

The margin of error of a contrast estimate

Now that we have obtained the error variance of a treatment effect by using a linear combination of mean squares and a Satterthwaite approximation of the degrees of freedom we are able to figure out the margin of error (MOE) of our contrast estimate. Just as in the simple between subjects design we discussed previously we obtain MOE by multiplying the standard error of the estimate with a critical value of t. The critical value of t is the .975 quantile of the central t-distribution with the Satterthwaite approximated degrees of freedom (if you are looking for something other than a 95% confidence interval, you will have to use another critical value, of course). The following code gives the critical value of t for a 95% confidence interval (change the value of C if you want something other than a 95% interval).

C = .95
alpha = 1 - C
critT = qt(1 - alpha/2, df)
critT

## [1] 2.025542

The standard error of the contrast estimate $\hat{\psi}$ can be obtained as follows.

$\hat{\sigma}_{\hat{\psi}}=\sqrt{\sum c_{i}^{2}\hat{\sigma}_{\bar{X},Rel}^{2}},$

where I have used the symbol $\sigma^2_{\bar{X},Rel}$ to refer to the relative error variance of the treatment mean (which in this design is equal to the absolute error variance, but that’s another story), and $c_i$ refers to the contrast weight of treatment mean i. The relative error variance of the treatment mean is obtained by dividing the error variance that is used to test the treatment effect by the total number of observations in each treament, $nm$ . Thus, using the results in Figure 1.

$\hat{\sigma}_{\bar{X},Rel}^{2}=\frac{MS_{p}+MS_{s}-MS_{e}}{nm}=\frac{15.07}{72}=0.2093.$

If we want to estimate an interaction contrast for the 2 x 2 design, we may, for example, specify contrasts weights ${1, -1, -1, 1}$ . Let’s use the results in Figure 1 to calculate what MOE is for this particular contrast.

#sample sizes per treatment
n = 12
m = 6

#obtained mean squares (see Figure 1): 
MSp = 6.403
MSs = 10.137
MSe = 1.470

#Relative error variance: 
VarT = (MSp + MSs - MSe) / (n*m)

#contrast weights: 
weights = c(1, -1, -1, 1)

#standard error of contrast estimate
SEcontrast = sqrt(sum(weights^2)*VarT)

#Satterthwaite degrees of freedom: 
dfp = 44
dfs = 20
dfe = 220
df = (MSp + MSs - MSe)^2 / (MSp^2/dfp + MSs^2/dfs + MSe^2/dfe)

#critical T 
critT = qt(.975, df)

#Margin of Error 
MOE = critT * SEcontrast

SEcontrast; MOE

## [1] 0.9149985

## [1] 1.853368

SPSS GLM Univariate uses the wrong standard error for a mixed model contrast estimate

Even though SPSS GLM Univariate allows you to specify a mixed model design and tests the treatment effect with a linear combination of mean squares, the procedure does not use the correct error variance if you want to estimate the value of a contrast (using the CONTRAST subcommand), it uses MSError instead. In our example, then, SPSS uses an error variance that is an order of magnitude smaller than the correct error variance: $1.47$ , with 220 degrees of freedom and not $15.07$ , with 37.357 (see Figure 1). The consequence of this is, of course, that the 95% CI is much narrower than it should be.

Running the syntax above Figure 1 gives the output in Figure 2. The results can be reproduced as follows. The standard error of the contrast is the result of $SE = \sqrt{\sum{c_i^2}\frac{MSe}{nm}} = \sqrt{4*1.47/72} = 0.2858$ , the critical value of t is the .975 quantile of the central t distribution with $df = 220$ , which equals $1.9708$ . The value of MOE is therefore $MOE = 0.5633$ . With a contrast estimate of $-0.587$ , the 95% CI equals $-0.587 \pm 0.5633 = [-1.1503, -0.0237]$ . In comparison, using the correct value of MOE gives us $[−2.4404, 1.2664]$ .

Figure 2: SPSS GLM Univariate Contrasts Output

Thus, even though SPSS GLM Univariate gives us the ingredients to work with, i.e. an estimate of the error variance and approximate degrees of freedom, it should not be used for obtaining contrast estimates if you have a mixed model. SPSS Mixed does a much better job and the MIXED output also contains other useful data we can use for sample size planning. (In practice, I use the linear mixed effects modeling package LME4) and not so much SPSS). Have a quick look at Figure 3 for the contrast estimate obtained with the mixed procedure. (Note how the numbers are essentially the same as the ones we obtained when using the ANOVA source table of SPSS GLM Univariate (Figure 1)).

MIXED score BY cond   
/CRITERIA=CIN(95) MXITER(100) MXSTEP(10) SCORING(1) 
SINGULAR(0.000000000001) HCONVERGE(0, ABSOLUTE) 
LCONVERGE(0, ABSOLUTE) PCONVERGE(0.000001, ABSOLUTE)   
/FIXED= cond | SSTYPE(3)   
/METHOD=REML  
/TEST= 'interaction' cond 1 -1 -1 1   
/RANDOM=INTERCEPT | SUBJECT(pp) COVTYPE(VC)  
/RANDOM=INTERCEPT | SUBJECT(ss) COVTYPE(VC).

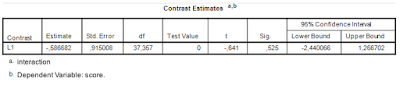Figure 3: Contrast Estimate SPSS Mixed

Planning for precision

Even though the result in Figure 3 is hard to interpret without substantive detail (the data are made up) it is clear that the precision of the estimate is, well, suboptimal. As an indication: the estimated within treatment standard deviaion is about 1.74, so the estimated difference between differences (interaction) is close to a value of Cohen’s d of $-.30$ , approximate 95% CI $[-1.40, 0.73]$ , which according to the rules of thumb is a medium negative effect, but consistent with anytihing from a huge negative effect to a large positive effect in the population, as the approximate CI shows. (I have divided the point estimate and the confidence interval in Figure 2 by 1.74, to obtain Cohen’s d and an approximate confidence interval). Clearly, then, our precision can be optimized.

Suppose that you are very fond of the both-within-condition design (BwC-design) and you plan to use it again in a replication study, You could of courseopt for a design with better expected precision, but based on the data and estimates at hand, that involves a lot of assumptions, but I will show you how you can do it in one of the next posts. If you plan for precision using the BwC-design, you need the following ingrediënts.

1. A figure for your target MOE. Let’s set target MOE to .40.

2. A specification of the percentage of assurance. Let’s say we want 80% assurance that target MOE will not exceed .40.

3. Estimates (or guesstimates) of the person variance $\sigma^2_p$ , the stimulus variance $\sigma^2_s$ , and the error variance $\sigma^2_e$ . We will have a look in the next section.

4. Functions for calculating the relative error variance, degrees of freedom, MOE and determining the required sample sizes for Participants and Stimuli. These are all present in the Precision App, so I will use the application, but I will show how the results of the sample sizes relate to the information above.

Obtaining estimates of the variance components

We need to specify the values of three variance components. These variance components can be estimated on the basis of the mean squares and sample sizes obtained with SPSS GLM Univariate, we can use SPSS MIXED to obtain direct estimates or any other way to estimate variance components, such as GLM VARCOMPS (which has several estimation procedures). I like to use SPSS MIXED or LME4. and not a dedicated program for variance components, because most of the times the main purpose of the analysis I am doing is obtaining contrast estimate or F-tests, so most of the times variance components estimates are a handy by-product of my main analysis. For demonstrative purposes, I will show how it can be done with the GLM univariate output and I will show how the results match those of SPSS MIXED.

Take a look at Figure 1. The estimate of $\sigma^2_e$ is simply MS(Error) = 1.47. For obtaining an estimate for the variance component associated with participants, we set the obtained mean square equal to the expected mean square (see Table 1). Thus, $6.403 = m\sigma^2_p + \sigma^2_e$ . Rearranging and using 1.47 as an estimate for $\sigma^2_e$ leads to $\sigma^2_p = (6.403 - \sigma^2_e) / m = (6.403 - 1.47) / 6 = 0.8222$ . Likewise, the estimate for $\sigma^2_s = (10.137 - 1.47) / 12 = .7223$ . Thus, our estimates are $\hat{\sigma}^2_e = 1.47$ , $\hat{\sigma}^2_p = 0.8222$ , and $\hat{\sigma}^2_s = 0.7223$ .

In order to obtain direct estimates you can use SPSS Mixed (or GLM Varcomps, or whatever you like). If you run the SPSS syntax in Figure 3, you will find estimates of the variance components under the heading Covariance Parameters in your SPSS output. See Figure 4. Note that the standard errors are pretty large, so the point estimates are not very precise. But since it is the only information we have, we will consider the point estimates to be the best we have.

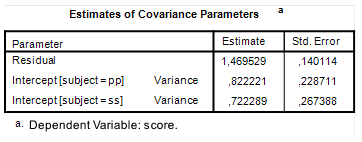Figure 4: Variance components estimates

Getting sample sizes with the Precision application

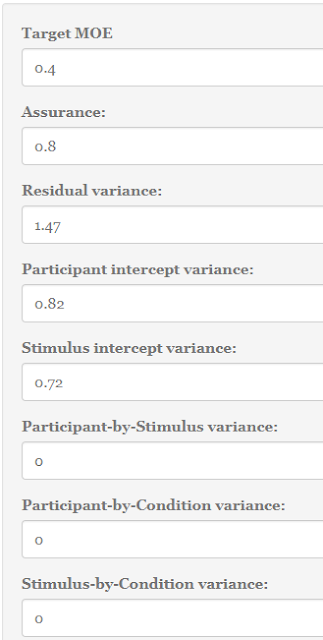Let’s use the Precision app (https://gmulder.shinyapps.io/precision/) for sample size planning. Set the design to Stimulus and Participant within condition, the number of conditions to 4 and in the options for contrast 3 fill in the weights ${1, -1, -1, 1}$ (Note: it is not necessary to fill it in in contrast 3).

For target MOE fill in $0.4$ , for assurance the value .80 and the values $1.47$ , $0.82$ , and $0.72$ for, respectively, Residual variance, Participant intercept variance and Stimulus intercept variance. Fill in the value 0 for all the other variances. See Figure 5.

Figure 5: Setting values in the Precision App.

Press the button “Get Sample Sizes”. The calculations take a while, so make yourself some coffee (or anything else you like) and when you return the screen should show something like Figure 6a.

Figure 6a: Output for planning target MOE = 0.40

Figure 6b: Outpur for planning target MOE = 0.50

By the way, if you wonder why you can simply set the three interaction variance components to zero, then it may be nice to know that the variance components estimates obtained from the both-within-condition design already include them. For example, the estimate of the resiidual variance obtained with the both-within-condition design is actually the sum of the residual variance component and the interaction conponent of participant and stimulus. These latter components can only be separated in a fully-crossed-design where all participants respond to all stimuli in all conditions. Thus, if we use the symbol $\sigma^2_{e, bwc}$ , to refer to the residual variance in the BwC-design, we can say $\sigma^2_{e, bwc} = \sigma^2_{ps} + \sigma^2_e$ . Normally, the precision app sums these two components to get a value for the residual variance in the BwC-design, and you will obviously get the same result if you specify the residual variance as the sum and the participant-by-stimulus variance as 0. Likewise, $\sigma^2_{p, bwc} = \sigma^2_p + \sigma^2_{cp}$ , and $\sigma^2_{s, bwc} = \sigma^2_s + \sigma^2_{cs}$ , where $\sigma^2_{cp}$ and $\sigma^2_{cs}$ are the variances associated with the interaction of treatment and participant and treatment and stimulus, respectively.

If you look at the sample sizes in Figure 6a, you may notice that the numbers look odd. For example, the app says that the smallest number of stimuli is 877 but it also says that you only need 500 stimuli if you select 802 participants. And something like that happens to the participants as well. The output says that the smaller number of participants is 802, but it also suggest using 500 of them if you use 877 stimuli, which is clearly smaller than 802. To me this seems a little inconsistent. But I think I figured out what’s going on. The reason for these inconsistencies is that the application minimizes the sample sizes, but with a maximum of 500 for the other sample sizes. So, the smallest number of stimuli is 877 given that the maximum number of participants is 500. In other words, a smaller sample size is possible, but then we have to increase the maximum number of participants. In other words, in order to have 80% assurance to obtain a target MOE of no more than .40, we need at least 500 stimuli or at least 500 participants. If you look at Figure 6b, you will not notice these inconsistencies. The difference between the left and right sample sizes is that sizes on the right are based on a target MOE of .50 instead of .40.

According to Figure 6a, we can obtain our target if we use 802 participants and 500 stimuli. Since we are planning for an experiment with 4 treatment conditions, these total sample sizes need to be divided by 4 to get the sample sizes per treatment conditions. Thus, n = 804/4 = 201 participants, and m = 500 / 4 = 125 stimuli per treatment condition (I’ve increased the participants sample size to make it divisible by 4). For many experiments these numbers are impractically large, of course, so in this case you would probably either consider an alternative design or else you have to live with the message that you may not get the precision you want or need.

Checking the sample size suggestions using what we know

If we fill in the sample sizes (802 participants and 500 stimuli) in the Precision app we get the results presented in Figure 7 for the interaction contrast (contrast 3). Expected MOE equals $0.3927$ , and there is 80% assurance that MOE will not exceed $0.4065$ . Note, again, that the assurance MOE is somewhat larger than target MOE, because a sample of 804 participants requires a sample of more than 500 stimuli to get the target MOE with 80% assurance and 500 stimuli is the maximum number of stimuli the app considers when minimizing the number of participants.

Figure 7: Expected and Assurance MOE for the interaction contrast (contrast 3) using 804 participants and 500 stimuli

Let’s see if we can reconstruct the figures using what we know from previous sections. First the relative error variance of the treatment mean. That relative error variance is $(m\sigma^2_p + n\sigma^2_s + \sigma^2_e)/ nm = 0.0099.$

The degrees of freedom can be calculated by first filling in the expected mean squares and the degrees of freedom presented in Table 1: $MS_p = 125*.82 + 1.47 = 103.96$ , $df_p = 800$ , $MS_s = 201*.72 + 1.47 = 146.19$ , $df_s = 496$ , $MS_e = 1.47$ , and $df_e = 4*(201 - 1)*(125 - 1) = 99200$ . The Satterthwaite degrees of freedom are $(MS_p + MS_s - MS_e)^2 / (MS_p^2/df_p + MS_s^2/df_s + MS_e^2/df_e) = 1092.66$ . The standard error of the contrast equals $\sqrt{4*.0099} = 0.1990$ . The critical value for t equals $1.9621$ . Expected MOE is, therefore, $0.3905$ (the tiny difference with the results from the app is due to rounding errors).

For the calculation of assurance MOE we need to take the sampling distribution of the relative error variance of the treatment mean into account. The app uses the (scaled) $\chi^2$ -distribution. That is, we assume with assurance $\gamma$ , that the $\gamma$ quantile of the sampling distribution of the relative error error variance is $\sigma^2_{\bar{X}, rel}*\chi^2_{\gamma, df}/df$ . Now, the degrees of freedom are $1092.66$ , the assurance $\gamma = .80$ , and the .80 quantile of $\chi^2$ with 1092.66 degrees of freedom equals $1131.7966$ . Since the relative error variance equals $0.0099$ , the .80 quantile of the error variance equals $0.0099*1131.7966/1092.66 = 0.0103$ . And this means that assurance MOE equals $1.9621*\sqrt{4*0.0103} = 0.3982$ . Again, the difference with the results from the Precision App are due to rounding error.

Month: December 2017

Planning for a precise contrast estimate: the mixed model case