In this post, I will introduce some of the ideas underlying sample size planning for precision. The ideas are illustrated with a shiny-application which can be found here: https://gmulder.shinyapps.io/PlanningApp/. The app illustrates the basic theory considering sample size planning for two independent groups. (If the app is no longer available (my allotted active monthly hours are limited on shinyapps.io), contact me and I’ll send you the code).
The basic idea
The population
In general, then, you should try to show (to others, if not to yourself) that it is reasonable to assume normally distributed populations, with equal variances and random sampling, before you decide that the p-value of your t-test, the width of your confidence interval, and the results of sample size calculations are believable.
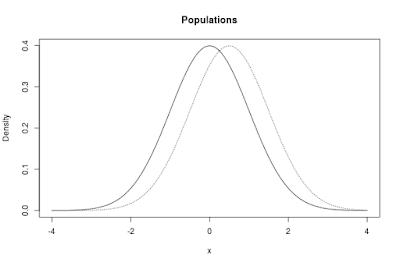
The populations in the app are normal distributions. By default, the app shows two such distributions. One of the distributions, the one I like to think about as corresponding to the control condition, has μ = 0, the other one has μ = 0.5. Both distributions have a standard deviation (σ = 1). The standardized difference between the means is therefore equal to δ = 0.50.
The default populations are presented in Figure 1 below.
The sampling distribution of the mean difference
The other default setting in the app is a sample size (per group) of n = 20. From the sample size and the specification of the populations, we can deduce the probability density of the different values of the estimates of the difference between the population means. The estimate is simply the difference between the sample means.
This so-called sampling distribution of the mean difference is depicted on the tab next to the population. Figure 2 shows what the sampling distribution looks like if we repeatedly draw random samples of size n = 20 per group from our populations and keep track of the difference between the sample means we get in each repetition.
 |
| Figure 2: Sampling distribution of the difference between two sample means based on samples of n = 20 per group and random sampling from the populations described in Figure 1. |
Note that the mean of the sampling distribution equals 0.5 (as indicated by the middle vertical line). This is of course the (default) difference between the population means in the app. So, on average, estimates of the population difference equal the population difference.
The lines to the left and the right of the mean indicate the mean plus or minus the Margin of Error (MOE). The values corresponding to the lines are 0.5 ± MOE. 95% of estimates of the population mean difference have a value between these lines.
Conceptually, the purpose of planning for precision is to decrease the (horizontal) distance between these lines and the population mean difference. In other words, we would like the left and right lines as close to the mean of the distribution as is practically acceptable and possible.
The distribution of the t-statistic
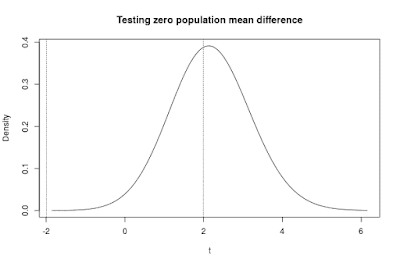
The tab next to the sampling distribution tab contains a figure representing the sampling distribution of the t-statistic. The sampling distribution of t can be deduced on the basis of the population values and the sample size. In the app, it is assumed that t is calculated under the assumption that the null-hypothesis of zero difference between the means is true. The sampling distribution of t is what you get if you repeatedly sample from the populations as specified, calculate the t-statistic and keep a record of the values of the t-statistic.
The sampling distribution of the t-statistic presented in Figure 3 contains two vertical lines. These lines are located (horizontally) on the value of t that would lead to rejection of the null-hypothesis of equal population means. In other words, the lines are located at the critical value of t (for a two-tailed test).
The area between the lines is the probability that the null-hypothesis will not be rejected. In the case of a true population mean difference (which is the default assumption in the app), that probability is the probability of an error of the second kind: a type II error.
The complement of that probability is called the power of the test. This is, of course, the area to the left of the left vertical line added to the area to the right of the right vertical line. Conceptually, the power of the test is the probability of rejecting the null-hypothesis when in fact it is false.
Figure 3 clearly demonstrates that if the true mean difference equals 0.50 and the sample size (per group) equals n = 20, that there is a large probability that the null-hypothesis will not be rejected. Actually, the probability of a type II error equals .66. (So, the power of the test is .34).
Sample size planning for precision
With respect to sample size planning for precision, the app by default takes half of a standard deviation (f = .50) as the target MOE. Besides, planning is with 80% assurance. This means that the default settings search for a sample size (per group), so that with 80% probability MOE will not exceed 0.50 (Note that the default value of the standard deviation is 1, so an f of .50 corresponds to a target MOE of 0.50 on the scale of the data; Likewise, were the standard deviation equal to 2, an f of .50 would correspond to a target MOE of 1.0).
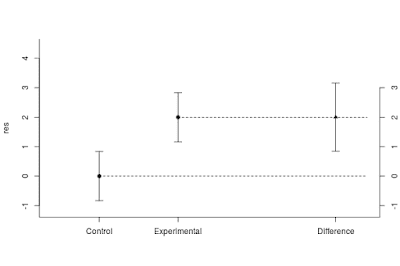
As described above, planning with the default values gives us a sample size of n = 37 per group, with an expected MOE of 0.46. In the tab next to the planning results, a figure displays what you can expect to find on average, given the planned sample size and the specification of the population. That figure is repeated here as Figure 4.
Figure 4 displays point and interval estimates of the group means and the difference between the means. The interval estimates are 95% confidence intervals. The figure clearly shows that on average, our estimate of the difference is very imprecise. That is, the expected 95% confidence interval ranges from almost 0 (0.50 – 0.46 = 0.04) to almost 1 (0.50 + 0.46 = 0.96). Of course, using n = 20, would be worse still.
A nice thing about the app (well, I for one think it’s pretty cool) is that as soon as you ask for the sample sizes, the sample size in the set population values form is automatically updated. Most importantly, this will also update the sampling distribution graphs of the difference between the means and the t-statistic. So, it provides an excellent way of showing what the updated sample size means in terms of MOE and the power of the t-test.
Let’s have a look at the sampling distribution of the mean difference, see Figure 5.
 |
| Figure 5: Sampling distribution of the mean difference with n = 37 per group. Compare with Figure 2 to see the (small) difference in the Margin of Error compared to n = 20. |
If you compare Figures 5 and 2, you see that the vertical lines corresponding to the mean plus and minus MOE have shifted somewhat towards the mean. So here you can see, that almost doubling the sample size (from 20 to 37) had the desired effect of making MOE smaller.
I would like to point out the similarity between the sampling distribution of the difference and the expected results plot in Figure 4. If you look at the expected results for our estimate of the population difference, you see that the point estimate corresponds to the mean of the sampling distribution, which is of course equal to the populations mean difference and that the limits of the expected confidence interval correspond to the left and right vertical lines in Figure 5. Thus, on average the limits of the confidence interval correspond to the values that mark the middle 95% of the sampling distribution of the samples mean difference.
Since we specified an assurance of 80%, there is an 80% probability that in repeated sampling from the populations (see Figure 1) with n = 37 per group, our (estimated) MOE will not exceed half a standard deviation. Thus, whatever the true value of the populations mean difference is, there is a high probability that our estimate will not be more than half a standard deviation away from the mean. This is, I think, one of the major advantages of sample size planning for precision: we do not have to specify the unknown population mean difference. This is in contrast to sample size planning for power, where we do have to specify a specific population mean difference.
Speaking of power, the results of the sample size planning suggest that for our specification of the populations mean difference (Cohen’s delta = 0.50) the power of the test equals 0.56. Thus, there is a probability of 56% that with n = 37 per group the t-test will reject. The probability of a type II error is therefore 44%.
Figure 6 shows the distribution of the t statistic with n = 37 per group and a standardized effect size of 0.50.
Power versus precision
Now suppose that the unstandardized mean difference between the population means equals 2 and that the standard deviation equals 2.5. I just filled in the set population values form, setting the mean of population 2 to 2.0 and the standard deviation to 2.5. And I clicked set values.
Let us plan for a target MOE of f = 0.5 standard deviations with 80% assurance. Click get sample sizes in the sample size planning form. In this case, target MOE equals 1.25.
The results are not very surprising. Since the f did not change compared to the previous time, the results as regards the sample size are exactly the same. We need n = 37. Again, this is what I like about sample size planning, no matter what the unknown situation in the population is, I just want my margin of error to be no more than half a standard deviation (for example).
But the power did change (of course). Since the standardized population mean difference is now 0.80 (= 2.0 / 2.5) in stead of 0.50, and all the other specifications remained the same, the power increases from 56% to 92%. That’s great.
However, the high probability of rejecting the null-hypothesis does not mean that we get precise estimates. On average, the point estimate of the difference equals 2 and the 95% confidence limits are 0.85 and 3.15 (the point estimate plus or minus 0.46 times the standard deviation of 2.5). See Figure 7.
In short, even though there is a high probability of (correctly) rejecting the null-hypothesis of equal population means, we are still not in the position to confidently conclude what the size of the difference is: the expected confidence interval is very wide.