Tag: NHST

Posted on

Planning for Precision: A confidence interval for the contrast estimate

In a previous post, which can be found here, I described how the relative error variance of a treatment mean can be obtained by combining variance components.  I concluded that post by mentioning how this relative error variance for the treatment mean can be used to obtain the variance of a contrast estimate. In this post, I will discuss a little more how this latter variance can be used to obtain a confidence interval for the contrast estimate, but we take a few steps back and consider a relatively simple study.

The plan of this post is as follows. We will have a look at the analysis of a factorial design and focus on estimating an interaction effect. We will consider both the NHST approach and an estimation approach. We will use both ‘hand calculations’ and SPSS.

An important didactic aspect of this post is to show the connection between the ANOVA source table and estimates of the standard error of a contrast estimate. Understanding that connections helps in understanding one of my planned posts on how obtaining these estimates work in the case of mixed model ANOVA.  See the final section of this post.


The data we will be analyzing are made up. They were specifically designed for an exam in one of the undergraduate courses I teach. The story behind the data is as follows.

Description of the study

A researcher investigates the extent to which the presence of seductive details in a text influences text comprehension and motivation to read the text. Seductive details are pieces of information in a text that are included to make the text more interesting (for instance by supplying fun-facts about the topic of the text) in order to increase the motivation of the reader to read on in the text. These details are not part of the main points in the text. The motivation to read on may lead to increased understanding of the main points in the text. However, readers with much prior knowledge about the text topic may not profit as much as readers with little prior knowledge with respect to their understanding of the text, simply because their prior knowledge enables them to comprehend the text to an acceptable degree even without the presence of seductive details.

The experiment has two independent factors, the readers’ prior knowledge (1 = Little,  2 =  Much) and the presence of seductive details (1 = Absent, 2 = Present) and two dependent variables, Text comprehension and Motivation.  The experiment has a between participants design (i.e. participant nested within condition).

The research question is how much the effect of seductive details differs between readers with much and readers with little prior knowledge. This means that we are interested in estimating the interaction effect of presence of seductive details and prior knowledge on text comprehension.

The NHST approach

In order to appreciate the different analytical focus between traditional NHST (as practiced) and an estimation approach, we will first take a look at the NHST approach to the analysis. It may be expected that researchers using that approach perform an ANOVA ritual as a means of answering the research question. Their focus will be on the statistical significance of the interaction effect, and if that interaction is significant the effect of seductive details will be investigated separately for participants with little and participants with much prior knowledge. The latter analysis focuses on whether these simple effects are significant or not. If the interaction effect is not significant, it will be concluded that there is no interaction effect. Of course, besides the interaction effect, the researcher performing the ANOVA ritual will also report the significance of the main effects and will conclude that main effects exist or not exist depending on whether they are significant or not. The more sophisticated version of NHST will also include an effect size estimate (if the corresponding significance test is significant) that is interpreted using rules of thumb. 
The two way ANOVA output (including partial eta squared) is as follows. 
indepedent factorial anova
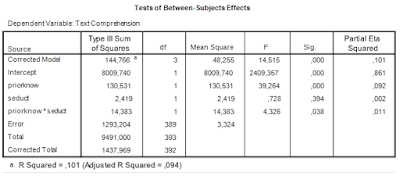Table 1. Output of traditional two-way ANOVA

The results of the analysis will probably be reported as follows.

There was a significant main effect of prior knowledge (F(1, 393) = 39.26, p < .001, partial η2 = .09). Participants with much prior knowledge had a higher mean text comprehension score than the participants with little prior knowledge.  There was no effect of the presence of seductive details (F < 1).  The interaction effect was significant (F(1, 393) = 4.33, p < .05, partial η2 = .01).

Because of the significant interaction effect, simple effects analyses  were performed to further investigate the interaction. These results show a significant effect of the presence of seductive details for the participants with little knowledge (p < .05), with a higher mean score in the condition with seductive details, but for the participants with much prior knowledge no effect of seductive details was found (p = .38), which explains the interaction. (Note: with a Bonferroni correction for the two simple effects analyses the p-values are p = .08 and p = .74; this will be interpreted as that neither readers with little knowledge nor with much knowledge benefit from the presence of seductive details).

The conclusion from the traditional analysis is that the effect of seductive details differs between readers with little and readers with much prior knowledge. The presence of seductive details only has an effect on the comprehension scores of readers with little prior knowledge of the text topic, in the presence of seductive details text comprehension is higher than in the absence of seductive details. Readers with much prior knowledge do not benefit from the presence of seductive details in a text.

Comment on the NHST analysis

The first thing to note is that the NHST conclusion does not really answer the research question. Whereas the research question ask how much the effects differ, the answer to the research question is that a difference exists. This answer is further specified as that there exists an effect in the little knowledge group, but that there is no effect in the much knowledge group. 
The second thing to note is that although there is a simple research questions, the report of the results includes five significance tests, while none of them actually address the research question. (Remember it is an how-much question and not a whether-question, the significance tests do not give useful information about the how-much question). 
The third thing to notice is that although effect sizes estimates are included (for the significant effects only) they are not interpreted while drawing conclusions. Sometimes you will encounter such interpretations, but usually they have no impact on the answer to the research question. That is, the researcher may include in the report that there is a small interaction effect (using rules-of-thumb for the interpretation of partial eta-squared; .01 = small; .06 = medium, .14 = large), but the smallness of the interaction effect does not play a role in the conclusion (which simply reformulates the (non)significance of the results without mentioning numbers; i.e. that the effect exists (or was found) in one group but not in the other). 

As an aside, the null-hypothesis test for the effect of prior knowledge i.e. that the mean comprehension score of readers with little knowledge are equal to the mean comprehension score of readers with much prior knowledge about the text topic seems to me an excellent example of a null-hypothesis that is so implausible that rejecting it is not really informative. Even if used as some sort of manipulation check the real question is the extent to which the groups differ and not whether the difference is exactly zero. That is to say, not every non-zero difference is as reassuring as every other non-zero difference: there should be an amount of difference between the groups below which the group performances can be considered to be practically the same. If a significance tests is used at all, the null-hypothesis should specify that minimum amount of difference.

Estimating the interaction effect

We will now work towards estimating the interaction effect. We will do that in a number of steps. First, we will estimate the value of the contrasts on the basis of the estimated marginal means provided by the two-way ANOVA and show how the confidence interval of that estimate can be obtained. Second, we will use SPSS to obtain the contrast estimate. 
Table 2 contains the descriptives and samples sizes for the groups and the estimated marginal means are presented in Table 3. 
Table 2. Descriptive Statistics
Table 3. Estimated Marginal Means

Let’s spend a little time exploring the contents of Table 3. The estimated means speak for themselves, hopefully. These are simply estimates of the population means.

The standard errors following the means are used to calculate confidence intervals for the population means. The standard error is based on an estimate of the common population variance (the ANOVA model assumes homogeneity of variance and normally distributed residuals). That estimate of the common variance can be found in Table 1: it is the Mean Square Error. Its estimated value is 3.32, based on 389 degrees of freedom.

The standard errors of the means in Table 3 are simply the square root of the Mean Square Error dvided by the sample size. E.g. the standard error of the mean text comprehension in the group with little knowledge and seductive details absent equals √(3.32/94) = .1879.

The Margin of Error needed to obtain the confidence interval is the critical t-value with 389 degrees of freedom (the df of the estimate of Mean Square Error) multiplied by the standard error of the mean. E.g. the MOE of the first mean is t.975(389)*.1879 = 1.966*.1879 = 0.3694.

The 95%-confidence interval for the first mean is therefore 3.67 +/- 0.3694 = [3.30, 4.04].

Contrast estimate

We want to know the extent to which the effect of seductive details differs between readers with little and much prior knowledge. This means that we want to know the difference between the differences. Thus, the difference between the means of the Present (P) and Absent (A) of readers with Much (M) knowledge is subtracted from the difference between the means of the  readers with Little (L) knowledge: (ML+P – ML+A) – (MM+P – MM+A) = ML+P – ML+A – MM+P + MM+A = 4.210 – 3.670 – 4.980 + 5.206 =  0.766.

Our point estimate of the difference between the effect of seductive details for little knowledge readers and for much knowledge is  that the effect is 0.77 points larger in the group with little knowledge.

For the interval estimate we need the estimated standard error of the contrast estimate and a critical value for the central t-statistic. To begin with the latter: the degrees of freedom are the degrees of freedom used to estimate Mean Square Error (df = 389; see Table 1).

The standard error of the contrasts estimate can be obtained by using the variance sum law. That is,  the variance of the sum of two variables is the sum of their variances plus twice the covariance. And the variance of the difference between two variables is the sum of the variances minus twice the covariance. In the independent design, all the covariances between the means are zero, so the variance of the interaction contrast is simply the sum of the variances over the means. The standard error is the square root of this figure. Thus, var(interaction contrast) = 0.1882 + 0.1822 + 0.1852 + 0.1812 = 0.1354, and the standard error of the contrast is the square root of  0.1354 = .3680.

Note that the we have squared the standard errors of the mean. These squared standard error are the same as the relative error variances of the means. (Actually, in a participant nested under treatment condition (a between-subject design) the relative error variance of the mean equals the absolute error variance). More information about the error variance of the mean can be found here: https://the-small-s-scientist.blogspot.nl/2017/05/PFP-variance-components.html.

The Margin of Error of the contrast estimate is therefore t.975(389)*.3680 = 1.966*.3680 = 0.7235. The 95% confidence interval for the contrast estimate is [0.04, 1.49].

Thus, the answer to the research question is that the estimated difference in effect of seductive details between readers with little prior knowledge and readers with much prior knowledge about the text topic equals .77, 95% CI [.04, 1.49].  The 95% confidence interval shows that the estimate is very imprecise, since the limits of the interval are .04, which suggests that the effect of seductive details is essentially similar for the different groups of readers, and 1.49, which shows that the effect of seductive details may be much larger for little knowledge readers than for much knowledge readers.

Analysis with SPSS

I think it is easiest to obtain the contrast estimate by modeling the data with one-way ANOVA by including a factor I’ve called ‘independent’. (Note: In this simple case, the parameter estimates output of the independent factorial ANOVA also gives the interaction contrast (including the 95% confidence interval), so there is no actual need to specify contrasts, but I like to have the flexibility of being able to get an estimate that directly expresses what I want to know). This factor has 4 levels: one for each of the combinations of the factors prior knowledge and presence of seductive details: Little-Absent (LA), Little-Present (LP),  Much-Absent (MA), and Much-Present (MP).

The interaction we’re after is the difference between the mean difference between Present and Absent for participants with little knowledge (MLP – MLA) and the mean difference between Present and Absent in the much knowledge group (MMP – MMA).  Thus, the estimate of the interaction (difference between differences) is (MLP – MLA) – (MMP – MMA) = MLP – MLA – MMP + MMA. This can be rewritten as 1*MLP + -1*MLA + -1*MMP + 1*MMA).

The 1’s and -1’s are of course the contrast weights we have to specify in SPSS in order to get the estimate we want. We will have to make sure that the weights correspond to the way in which the order of the means is represented internally in SPSS. That order is LA, LP, MA, MP.  Thus, the contrast weights need to be specified in that order to get the estimate to express what we want in terms of the difference between differences. See the second line in the following SPSS-syntax.

UNIANOVA comprehension BY independent
  /CONTRAST(independent)=SPECIAL ( -1 1 1 -1)
  /METHOD=SSTYPE(3)
  /INTERCEPT=INCLUDE
  /EMMEANS=TABLES(independent)
  /PRINT=DESCRIPTIVE
  /CRITERIA=ALPHA(.05)
  /DESIGN=independent.

The relevant output is presented in Table 4. Note that the results are the same as the ‘hand calculations’ described above (I find this very satisfying).

Table 4. Interaction contrast estimate

Comment on the analysis 

First note that the answer to the research question has been obtained with a single analysis. The analysis gives us a point estimate of the difference between the differences and a 95% confidence interval. The analysis is to the point to the extent that it gives the quantitative information we seek. 
However, although the estimate of the difference between the differences is all the quantitative information we need to answer the how-much-research question, the estimate itself obscures the pattern in the results, in the sense that the estimate itself does not tell us what may be important for theoretical or practical reasons, namely the direction of the effect.  That is, a positive interaction contrast may indicate the difference between an estimated positive effect for one group and an estimated negative effect  in the other group (which is actually the situation in the present example: 0.54 – (-0.23) = 0.77) in the other group). 
Of course, we could argue that if you want to know the extent to which the size and direction differ between the groups, then that should be reflected in your research question, for instance, by asking about and estimating the simple effects themselves in stead of focusing on the size of the difference alone, as we have done here. 

On the other hand, we could argue that no result  of a statistical analysis should be interpreted in isolation. Thus, there is no problem with interpreting the estimate of 0.77 while referring to the simple effects: the estimated difference between the effects is .77,  95% CI [.04, 1.49], reflecting the difference between an estimated effect of 0.54 in the little knowledge group and an estimated negative effect of -0.23 for much knowledge readers.

But, if the research question is how large is the effect of seductive details for little knowledge readers and high knowledge readers and how much do the effect differ, than that would call for three point estimates and interval estimates. Like: the estimated effect for the little knowledge group equals 0.54. 95% CI [0.03, 1.06], whereas the estimated effect for the much knowledge groups is negative -0.23, 95% CI [-0.73, 0.28]. The difference in effect is therefore 0.77,  95% CI [.04, 1.49].

In all cases, of course, the intervals are so wide that no firm conclusions can be drawn. Consistent with the point estimates are negligibly small positive effects to large positive effects of seductive details for the little knowledge group,  small positive effects to negative effects of seductive details for the much knowledge group and an interaction effect that ranges from negligibly small to very large. In other words, the picture is not at all clear.  (Interpretations of the effect sizes are based on rules of thumb for Cohen’s d. A (biased) estimate of Cohen’s d can be obtained by dividing the point estimate by the square root of Mean Square Error. An approximate confidence interval can be obtained by dividing the end-points of the non-standardized confidence intervals by the square root of Mean Square Error). Of course, we have to keep in mind that 5% of the 95% confidence intervals do not contain the true value of the parameter or contrast we are estimating.

Compare this to the firm (but unwarranted) NHST conclusion that there is a positive effect of seductive details for little knowledge readers (we don’t know whether there is a positive effect, because we can make a type I error if we reject the null) and no effect for much knowledge readers. (Yes, I know that the NHST thought-police forbids interpreting non-significant results as “no effect”, but we are talking about NHST as practiced and empirical research shows that researchers interpret non-significance as no effect).

In any case, the wide confidence intervals show that we could do some work for a replication study in terms of optimizing the precision of our estimates. In a next post, I will show you how we can use our estimate of precision for planning that replication study.

Summary of the procedure

In (one of the next) posts, I will show that in the case of mixed models ANOVA’s we frequently need to estimate the degrees of freedom in order to be able to obtain MOE for a contrast. But the basic logic remains the same as what we have done in estimating the confidence interval for the interaction contrast.  Please keep in mind the following. 
Looking at the ANOVA source table and the traditional ANOVA approach we notice that the interaction effect is tested against Mean Square Error: the F-ratio we use to test the null-hypothesis that both Mean Squares (the interaction MS an Mean Square Error) estimate the common error variance. The F-ratio is formed by dividing the Mean Square associated with the interaction by Mean Square Error.  The probability distribution of that ratio is an F-distribution with 1 (numerator) and 389 (denominator) degrees of freedom. 
Mean Square Error is also used to obtain the estimated standard error for the interaction contrast estimate. In the calculation of MOE, the critical value of t was determined on the basis of the degrees of freedom of Mean Square Error. 
This is the case in general: the standard error of a contrast is based on the Mean Square Error that is also used to test the corresponding Effect (main or interaction) in an F-test. In a simple two-way ANOVA the same Mean Square Error is used to test all the effects (main an interaction), but that is not generally the case for more complex designs. Also, the degrees of freedom used to obtain a critical t-value for the calculation of MOE are the degrees of freedom of the Mean Square Error used to test an effect. 
In the case of a mixed model ANOVA, it is often the case that there is no Mean Square Error available  to directly test an effect. The consequence of this is that we work with linear combinations of Mean Squares to obtain a suitable Mean Square Error for an effect and that we need to estimate the degrees of freedom. But the general logic is the same: the Mean Square Error that is obtained by a linear combination of Mean Squares is also used to obtain the standard error for the contrast estimate and the estimated degrees of freedom are the degrees of freedom used to obtain a critical value for t in the calculation of the Margin of Error. 
I will try to write about all of that soon. 
Posted on

What is NHST, anyway?

I am not a fan of NHST (Null Hypothesis Significance Testing). Or maybe I should say, I am no longer a fan. I used to believe that rejecting null-hypotheses of zero differences based on the  p-value was the proper way of gathering evidence for my substantive hypotheses. And the evidential nature of the p-value seemed so obvious to me, that I frequently got angry when encountering what I believed were incorrect p-values, reasoning that if the p-value is incorrect, so must be the evidence in support of the substantive hypothesis. 
For this reason, I refused to use the significance tests that were most frequently used in my field, i.e. performing a by-subjects analysis and a by-item analysis and concluding the existence of an effect if both are significant,  because the by-subjects analyses in particular regularly leads to p-values that are too low, which leads to believing you have evidence while you really don’t.  And so I spent a huge amount of time, coming from almost no statistical background – I followed no more than a few introductory statistics courses – , mastering mixed model ANOVA and hierarchical linear modelling (up to a reasonable degree; i.e. being able to get p-values for several experimental designs).  Because these techniques, so I believed, gave me correct p-values. At the moment, this all seems rather silly to me. 
I still have some NHST unlearning to do. For example, I frequently catch myself looking at a 95% confidence interval to see whether zero is inside or outside the interval, and actually feeling happy when zero lies outside it (this happens when the result is statistically significant). Apparently, traces of NHST are strongly embedded in my thinking. I still have to tell myself not to be silly, so to say. 
One reason for writing this blog is to sharpen my thinking about NHST and trying to figure out new and comprehensible ways of explaining to students and researchers why they should be vary careful in considering NHST as the sine qua non of research. Of course,  if you really want to make your reasoning clear, one of the first things you should do is define the concepts you’re reasoning about. The purpose of this post is therefore to make clear what my “definition” of NHST is. 
My view of NHST  is very much based on how Gigerenzer et al. (1989) describe it: 
“Fisher’s theory of significance testing, which was historically first, was merged with concepts from the Neyman-Pearson theory and taught as “statistics” per se. We call this compromise the “hybrid theory” of statistical inference, and it goes without saying the neither Fisher nor Neyman and Pearson would have looked with favor on this offspring of their forced marriage.” (p. 123, italics in original). 
Actually, Fisher’s significance testing and Neyman-Pearson’s hypothesis testing are fundamentally incompatible (I will come back to this later), but almost no texts explaining statistics to psychologists “presented Neyman and Pearson’s theory as an alternative to Fisher’s, still less as a competing theory. The great mass of texts tried to fuse the controversial ideas into some hybrid statistical theory, as described in section 3.4. Of course, this meant doing the impossible.” (p. 219, italics in original). 
So, NHST is an impossible, as in logically incoherent, “statistical theory”, because it (con)fuses concepts from incompatible statistical theories. If this is true, which I think it is, doing science with a small s, which involves logical thinking, disqualifies NHST as a main means of statistical inference. But let me write a little bit more about Fisher’s ideas and those of Neyman and Pearson, to explain the illogic of NHST. 

I will try to describe the main characteristics of  the two approaches that got hybridized in NHST at a conceptual level. I will have to simplify a lot and I hope these simplifications do little harm. Let’s start with Fisher’s significance testing. 

Fisher’s significance testing

The main purpose of Fisher’s significance testing is gathering evidence about parameters in a statistical model on the basis of a sample of data. So, the nature of the approach is evidential. Crucially, the evidence the data provides can only be evidence against a statistical model, but it can not be evidence in favour of the model, much in line with Popper’s idea  of progress in science by means of falsification. The statistical model to be nullified, i.e. the model one tries to obtain evidence against, is called the null-hypothesis.

Conceptually, the statistical model is a descriptive model of a population of possible values. An important part of Fisher’s approach is therefore to judge what kind of model provides an appropriate model of the population. For instance, this process of formulating the model (which, of course, involves a lot of thought and judgement) may lead one to assume that the random variable has a normal distribution, which is characterized by only two parameters, μ the expected value or mean of the distribution and σ, the square root of the variance of the distribution, which in the case of the normal distribution is it’s standard deviation (the standard deviation is the square root of the variance).

The values of μ and σ (or σ2) are generally unknown, but we may assume (again as a result of thinking and judging) that they have particular values. For reasons of exposition, I will now assume that the value of σ is known, say σ = 15, so that we only have to take the unknown value of μ into account. Let’s suppose that our thinking and judging has led us to assume that the unknown value of μ = 100.  The null-hypothesis is therefore that the variable has a normal distribution with μ = 100, and σ = 15.

We can obtain evidence against this null-hypothesis, by determining a p-value. We first gather data, say we take a random sample of N = 225 participants, which enables us to obtain observed values of the variable. Next, we calculate a test statistic, for example by estimating the value of  μ (on the basis of our data) subtracting the hypothesized value and dividing the estimate by it’s standard error. Our estimated value may for example be 103, and the standard error equals 15 / √225 = 1.0, so the value of the test statistic equals (103 – 100) / 1 = 3. And now we are ready to calculate the p-value.

The p-value is the probability of obtaining (when sampling repeatedly) a value of the test statistic as large as or larger than the one obtained in the study, provided that the null-hypothesis is true. This probability can be calculated because the exact distribution of the test statistic can be deduced from the specification of the null-hypothesis. In our example, the test statistic is approximately normally distributed with μ = 0, and σ = 1.0. (The distribution is approximately normal, assuming the null-hypothesis is true, so the p-value in our example not exact). The p-value equals 0.003. (This is the so-called two-sided p-value, it is the probability of obtaining a value equal or larger than 3 or equal of smaller than -3, but we will ignore the technicalities of two-sided tests).

The p-value tells us that if the null-hypothesis is true, and we repeatedly take random samples from the population (as described by the null-hypothesis) we will find a value of our test statistic or a larger value in 0.3% of these samples. Thus, the probability of obtaining a value equal to or larger than 3.0 is very small.

Following Fisher, this low p-value can be interpreted as that something “improbable” occurred (assuming the null-hypothesis is true) or as inductive evidence against the null-hypothesis, i.e. the null-hypothesis is not true. 

In his early writings Fisher proposed a p-value smaller than .05 as inductive evidence against the null-hypothesis (keeping in mind the possibility that the null is true, but that something improbable happened), but later he thought using the fixed criterion of .05 to be non-scientific.  If the p-value is smaller than the criterion (say .05), the result is statistically significant.
In sum, the approach by Fisher, significance testing, involves specifying a statistical model, and using the p-value to test the assumptions of the model, such as specific values for μ or σ. If the p-value is smaller than the criterion value, either something improbable occurred or the null-hypothesis is not true. Crucially, the p-value may provide inductive evidence against the assumptions of the null-hypothesis, but a large p-value (larger than the criterion value) is not inductive support for the null-hypothesis.

 

Neyman-Pearson hypothesis testing

In contrast to Fisher’s evidential approach, Neyman and Pearson’s hypothesis testing is non-evidential.  Its primary goal is to choose on the basis of repeated random sampling between two hypotheses (or more; but I will only consider two)  in order to make behavioral decisions (so to speak) that will minimize decision errors and their associated costs (loss) in the long run. In stead of trying to figure out which of the two hypotheses is true, one decides to accept  one (and reject the other) of the two hypothesis as if it were true, without actually having to believe it, and act accordingly. 
As with Fisher, Neyman-Pearson hypothesis testing starts with formulating descriptive models of the population. We may for instance propose (after thinking and judging) that one model (hypothesis H1) assumes that the variable has a normal distribution with μ = 100 and one model (hypothesis H2) that assumes that the variable has a normal distribution with μ = 106.  We will assume the value of σ is known, say it equals 15.  We will have to choose one of the two hypothesis, by rejecting one (and accepting the other).

Let’s suppose that only one of the models is true and that they cannot both be false. This means that we can incorrectly decide to reject or accept each of the two hypotheses.  That is, if we incorrectly reject H1, we incorrectly accept H2. So, there are two types of errors we can make. A type I error occurs when we incorrectly reject a true hypothesis and a type II error occurs when we incorrectly accept a false hypothesis.

In a previous post (here), I used the following conceptual descriptions of these errors: the type I error is the error of excessive skepticism, and the type II error is the error of  extreme gullibility, but from the perspective of Neyman-Pearson hypothesis testing these conceptual descriptions may not make much sense, because these terms imply a relation between the decisions about a hypothesis and belief in the hypothesis, while in the Neyman-Pearson approach a rejection or non-rejection does not lead to commitment in believing or not believing the hypothesis, although the hypotheses themselves are based on beliefs (and judging and reasoning) that the descriptive model is suitable for the population at hand. 
The crucial point is that the goal of Neyman-Pearson hypothesis testing is to base courses of action on the decision to reject or not-reject a statistical hypothesis. This entails minimizing the costs (loss) associated with type I and type II errors. In particular, the approach minimizes the probability (β) of a type II error bounded by the probability (α) of a type I error. We may also say that we want to maximize the probability (1 – β), the probability of rejecting a false hypothesis, the so called power of the test, while keeping α at a maximum (usually low) value. 
Suppose, that our considerations of the loss associated with type I and type II errors, has led us to the insight that false rejection of  H2 is the most costly error. And suppose that we have agreed/determined/reasoned/judged that the probability of falsely rejecting it should be at most .05. So, α = .05. Of course, we also  “know” the loss associated with falsely accepting it, and we have determined that the probability β should not exceed .10. Now, suppose that we repeatedly sample N = 225 observations from the (unknown) population. We do not know whether H1 or H2 provides the correct description of the population, but we assume that one of them must be true if we select a particular sample, and they cannot both be false.

We will reject H2 (Normal distribution with μ = 106, and σ = 15) if the sample mean in our random sample equals 104.35 or less (this corresponds to a test statistic with value -1.65).  Why, because the probability of obtaining a sample mean equal or smaller than 104.35 is approximately .05 when H2 is true. Thus, if we repeatedly sample from the population when H2 is true, we will incorrectly reject it in 5% of the cases. Which is the probability of a type I error that we want.

We have arranged things so, that when H2 is false, H1 is per definition true. If H1 is true (H2 is false), there is a probability of approximately .99 to obtain a sample mean of 104.35 or smaller. Thus, the probability to reject H2 when it it false is .99, this is the power of the test, and the probability is approximately .01 of incorrectly not rejecting H2 when it is false. The latter probability is the probability of a type II error, which we did not want to be larger than .10.

Now suppose the results is that the sample mean equals 103 (the value of the test statistic equals -3). According to the decision criterion we reject H2 (with α = .05) and accept H1 and act as if μ = 100 is true. Crucially, we do not have to believe it is actually true, nor do we consider the test statistic with value -3 as inductive evidence against H2. So, the test result provides neither support for H1 nor evidence against H2, but we know from the specification of the models and the assumptions about sampling that repeatedly using this procedure leads to 5% type I errors and 1%  type II errors in the long run, depending on which of the two hypotheses is true (which is unknown to us).  Given that we know the loss associated with each error, we are able to minimize the expected loss associated with acting upon the decisions we make about the hypotheses.

Note that Fisher’s significance testing would consider the p-value associated with the test statistic of -3, i.e. p < .01 either as inductive evidence against H2 or as an indication that something unusual (improbable) happened assuming H2 is true. Note also that in Fisher’s approach, it is not possible to reason from the inferred untruth of H2 to the truth of H1, because H1 does not exist in that approach.

It should be noted further that in the Neyman-Pearson approach, the importance of the value of the test statistic is restricted to whether or not the value exceeds a critical value (i.e. whether or not the value of the statistic is in the rejection region). That means that it is of no concern how much the test statistic exceeds the critical value, since all values larger than the critical value lead to the same decision: reject the hypothesis. In other words, because the approach is non-evidential, the magnitude of the test statistic is inconsequential as far as the truth of the hypothesis is concerned. Compare this to the Fisher approach, where the larger the test statistic is (the smaller the p-value), the stronger the inductive evidence is against the null-hypothesis.

Null-hypothesis significance testing (NHST)

NHST combines Fisher’s significance testing with Neyman-Pearson hypothesis testing, without regard for the logical incompatibilities of the two approaches. Fisher’s p-value is used both as a measure of inductive evidence against the null-hypothesis, with smaller p-values considered to be stronger evidence against the null than larger p-values, and as a test statistic. In its latter use, the null-hypothesis is (usually) rejected if the p-value is smaller than .05.

Contrary to significance testing, NHST uses the p-value to decide between the null-hypothesis and an alternative hypothesis. But contrary to the Neyman-Pearson approach, α, the probability of a type I error is not based on judgement and careful consideration of loss-functions, but is mechanically set at .05 (or .01). And, contrary to the Neyman-Pearson approach, the probability of a type II error (β) is usually not considered.

One reason for the latter may be that specification of the null-hypothesis is also mechanized.  In the case of differences between means or testing correlations or regression coefficients, etc, the standard null-hypothesis is that the difference, the correlation or the coefficient equals 0. This is also called the nil-hypothesis. As the alternative excludes the null, the standard alternative hypothesis is that the parameter in question is not equal to zero, which makes it hard to say something about the type II error, because determining the probability of a type II error requires thinking about a minimal consequential effect size (consequential in terms of decisions and associated loss) that can serve as the alternative hypothesis.

Specifying a non-nil alternative hypothesis, i.e. that the parameter value is not equal to zero, implies that results arbitrarily close to nil, but not equal to nil, are as consequential as effect sizes that are far away from the null-value, both in acting upon the value as in not-acting upon it. Crucially, not specifying a minimal consequential effect size, rules out determining  β. So, even though NHST uses the concept of an alternative hypothesis (contrary to Fisher), the nil-hypothesis is such that the procedure of Neyman and Pearson can no longer work: it is impossible to strike a balance between loss associated with type I and type II errors, and so NHST is not a hypothesis testing procedure.

For these reasons I am very much inclined to characterize NHST as fixed-α significance testing. But using fixed-α in combination with an evidential interpretation of p-values leads to logical inconsistencies. (As always, I assume that being logically consistent is one of the characteristics of doing science, but maybe you disagree). Note, by the way, that I am talking about the p-value as measure of evidence against the nil-hypothesis, and not about the p-value as test statistic. (But remember that proper use of the p-value as test statistic requires being able to specify a non-nil alternative hypothesis). 
One of the logical inconsistencies is that α and the p-value-as-evidence involve contradictory conceptualisations of probability.  In terms of p-values, α is simply the probability that the p-value is smaller than .05 (the usual criterion) assuming the nil-hypothesis is true. That probability follows deductively from the specification of the null-hypothesis (including, of course,  the statistical model underlying it). Note that α is completely independent of actually realized results: it an assertion about the p-value assuming repeated sampling from the null-population; α is about the test-procedure and not about actual data.
But the p-value-as-evidence against the null is not the result of deductive reasoning, but of inductive reasoning. The p-value is not a probability associated with the test-procedure. It is a random variable the value of which depends on the actual data, the null-value and the statistical model. Crucially, from a single realized result (a p-value) an inference is made about a probability distribution. But this is inconsistent with the frequency interpretation of probability that underlies the conceptualisation of α, because under this interpretation no probability statement can be made about realized single results (except that the probability is 100% that it happened) or about an unrealized single result (that probability is 0 if it does not happen or 1.0 if it happens).  To make the point: using p-value-as-evidence and (fixed)-α requires both believing that probability statements can be made on the basis of a single result and believing that that is impossible.  So, it boils down to believing that both A and not-A are true. 
To me, logical inconsistencies like these disqualify NHST as a scientific means of statistical inference. I repeat that this is because I believe that doing science entails being logically consistent. Assuming or believing that A and not-A are both true, is not an example of logical consistency.
Posted on

Lazy Larry’s argument and the Mechanical Mind’s reply

Meet Lazy Larry, the non-critically thinking reviewer of your latest experimental result. (The story also applies to Lazy Larry’s reviews of non-experimental results). Lazy Larry does not believe your results signify anything “real”. Never mind your excellent experimental procedures and controls, and forget about your highly reliable instruments, Lazy Larry refuses to think about your results and by default dismisses them as “due to chance”.

“Due to chance” is simply a short-hand description of, say, your experimental group seems to outperform the control group on average, but that is not due to your experimental manipulation, but due to sampling error: you just happened to have randomly assigned better performing participants to the experimental group than to the control group.

Enter the Mechanical Mind. Its sole purpose is to persuade Lazy Larry that the results are not “due to chance”. Mechanical Mind has learned that Lazy Larry is quite easily persuaded (remember that Larry doesn’t think), so Mechanical Mind always does the following:

  1. He pretends to have randomly assigned a random sample of participants to either the experimental or the control group. (Note the pretending is about having drawn a random sample; but since we assume an excellent experiment, we may just as well assume that the sample is in fact a random sample, but the Mechanical Mind always assumes a random sample, as part of its test procedure, even if the sample is a convenience sample). 
  2. He formulates a null-hypothesis that the mean population values are exactly equal to the millionth or more decimal. 
  3. He calculates a test statistic, say a t-value. 
  4. He determines a p-value:  the probability of obtaining a t-value as large as or larger than the one obtained in the experiment, under the pretense of repeated sampling from the population, assuming the null-hypothesis is true. 
  5. He rejects the null-hypothesis if the p-value is smaller than .05 and calls that result significant. 
  6. He concludes that the results are not “due to chance” and automatically takes that conclusion to mean that the effect of the experimental manipulation is “real.”

Being a non-thinker, Lazy Larry immediately agrees: if the p-value is smaller than .05, the effect is not “due to chance”, it is a real effect.

Enter a Small s Scientist. The Small s Scientist notices something peculiar. She notices that both Lazy Larry and the Mechanical Mind do not really think, which strikes her as odd. Doesn’t science involve thinking? Here we have Larry who has only one standard argument against any experimental result, and here we have the Mechanical Mind who has only one standard reply: a mindlessly performed ritual of churning out a p-value. Yes, it may shut up Lazy Larry, if the p-value happens to be smaller than .05, but the Small s Scientist is not lazy, she really thinks about experimental results.

She wonders about Lazy Larry’s argument. We have an experiment with excellent experimental procedures and controls, with highly reliable instruments, so although sampling error always has some role to play, it doesn’t immediately come to mind as a plausible explanation for the obtained effect. Again, simply assuming this by-default, is the mark of an unthinking mind.

She thinks about the Mechanical Minds procedure.  The Mechanical Mind assumes that the mean population values are completely equal up to the millionth decimal or more. Why does the Mechanical Mind assume this?  Is it really plausible that it is true? To the millionth decimal? Furthermore, she realizes that she has just read the introduction section of your paper in which you very intelligently and convincingly argue that your independent variable must have a major role to play in explaining the variation in the dependent variable. But now we have to assume that the population means are exactly the same? Reading your introduction section makes this assumption highly implausible.

She recognizes that the Mechanical Mind made you do a t-test. But is the t-test appropriate in the particular circumstances of your experiment? The assumptions of the test are that you have sampled from a normally distributed population with equal variance. Do these assumptions apply? The Mechanical Mind doesn’t seem to be bothered much about these assumptions at all. How could it? It cannot think.

She notices the definition of the p-value. The probability of obtaining a value of, in this case, the t-statistic as large as or larger than the one obtained in the experiment, assuming repeated random sampling from a population in which the null-hypothesis is true. But wait a minute, now we are assigning a probability statement to an individual event (i.e. the obtained t-statistic). Can we do that? Doesn’t a frequentist conception of probability rule out assigning probabilities to single events? Isn’t the frequentist view of probability restricted to the possibly infinite collection of single events and the frequency of occurrence of the possible values of the dependent variable? Is it logically defensible to assign probabilities to single events and at the same time make use of a frequentist conception of probability? It strikes the Small s Scientist as silly to think it is.

She understands why the Mechanical Mind focuses on the probability of obtaining results (under repeated sampling from the null-population) as extreme as or extremer than the one obtained. It is simply that any obtained result has a very low probability (if not 0; e.g. if the dependent variable is continuous), no matter the hypothesis.  So, the probability of a single obtained t-statistic is so low to be inconsistent with every hypothesis.  But why, she wonders, do we need to consider all the results that were not obtained (i.e. the more extreme results) in determining whether a “due to chance” explanation has some plausibility (remember that the “due to chance” argument does not seem to be very plausible to begin with)? Why, she wonders, do we not restrict ourselves to the data that were actually obtained?

The Small s Scientist gets a little frustrated when thinking about why a null-hypothesis can be rejected if p < .05 and not when p > .05. What is the scientific justification of using this criterion? She has read a lot about statistics but never found a justification of using .05, apart from Fisher claiming that .05 is convenient, which is not really a justification. It doesn’t seem to be very scientific to justify a critical value simply by saying that Fisher said so. Of course, the Small s Scientist knows about decision procedures a la Neyman and Pearson’s hypothesis testing in which setting α can be done on a rational basis by considering loss functions, but considering loss functions is not part of the Mechanical Mind’s procedure. Besides, is the purpose of the Mechanical Mind’s procedure not to counter the “due to chance” explanation, by providing evidence against it, in stead of deciding whether or not the result is due to chance? In any case, the 5% criterion is an unjustified criterion, and using 5% by-default is, let’s repeat it again, the mark of an unthinking mind.

The final part of the Mechanical Mind’s procedure strikes the Small s Scientist as embarrassingly silly. Here we see a major logical error. The Mechanical Mind assumes, and Lazy Larry seems to believe, that a low p-value (according to an unjustified convention of .05) entails that results are not “due to chance” whereas a high p-value means that the results are “due to chance”, and therefore not real. Maybe it should not surprise us that unthinking minds, mechanical, lazy, or both, show signs of illogical reasoning, but it seems to the Small s Scientist that illogical thinking has no part to play in doing science.

The logical error is the error of the transposed conditional. The conditional is: If the null-hypothesis (and all other assumptions, including repeated random sampling) is/are true, the probability of obtaining a t-statistic as large as or larger than the one obtained in the experiment is p. That is, if all of the obtained t-statistics in repeated samples are “due to chance”, the probability of obtaining one as large as or larger than the one obtained in the experiment equals p.  It’s incorrect transpose is: if the p-value is small, than the null-hypothesis is not true (i.e. the results are not “due to chance”).  Which is very close to: If the null-hypothesis is true, these results (or more extreme results) do not happen very often” to  “If these results happen, the null-hypothesis is not true”.  More abstractly the Mechanical Mind goes from “If H, than probably not R” to “If R, than probably not H”, where R stands for results and H for the null-hypothesis.”.

To sum up. The Small s Scientist believes that science involves thinking. The Mechanical Mind’s procedure is an unthinking reply to Lazy Larry’s standard argument that experimental results are “due to chance”. The Small s Scientist tries to think beyond that standard argument and finds many troubling aspects of the Mechanical Mind’s procedure. Here are the main points.

  1. The plausibility of the null-hypothesis of exactly equal population  means can not be taken for granted. Like every hypothesis it requires justification.
  2. The choice for a test statistic can not be automatically determined. Like every methodological choice it requires justification. 
  3. The interpretation of the p-value as a measure of evidence against the “due to chance” argument requires assigning a probability statement to a single event. This is not possible from a frequentist conception of probability. So, doing so, and simultaneously holding  a frequentist conception of probability means that the procedure is logically inconsistent. The Small s Scientist does not like logical inconsistency in scientific work. 
  4.  The p-value as a measure of evidence, includes “evidence” not actually obtained. How can a “due to chance” explanation (as implausible as it often is) be discredited on the basis of evidence that was not obtained? 
  5. The use of a criterion of .05 is unjustified, so even if we allow logical inconsistency in the interpretation of the p-value (i.e. assigning a probability statement to a single event), which a Small s Scientist does not, we still need a scientific justification of that criterion. The Mechanical Mind’s procedure does not provide such a justification. 
  6. A large p-value does not entail that the results “are due to chance”.  A p-value cannot be used to distinguish “chance” results from “non-chance” results. The underlying reasoning is invalid, and a Small s Scientist does not like invalid reasoning in scientific work. 
Posted on

Decisions are not evidence

The thinking that lead to this post began with trying to write something about what Kline (2013) calls the filter myth. The filter myth is the arguably – in the sense that it depends on who you ask – mistaken belief in NHST practice that the p-value discriminates between effects that are due to chance (null-hypothesis not rejected) and those that are real (null-hypothesis rejected). The question is whether decisions to reject or not reject can serve as evidence for the existence of an effect.

Reading about the filter myth made me wonder whether NHST can be viewed as a screening test (diagnostic test), much like those used in medical practice. The basic idea is that if the screening test for a particular condition gives a positive result, follow-up medical research will be undertaken to figure out whether that condition is actually present. (We can immediately see, by the way, that this metaphor does not really apply to NHST, because the presumed detection of the effect is almost never followed up by trying to figure out whether the effect actually exists, but the detection itself is, unlike the screening test, taken as evidence that the effect really exists; this is simply the filter myth in action).

Let’s focus on two properties of screening tests. The first property is the Positive Likelihood Ratio (PLR). The PLR is the ratio of the probability of a correct detection to the probability of a false alarm. In NHST-as-screening-test, the PLR  equals the ratio of the power of the test to the probability of a type I error: PLR = (1 – β) / α. A high value of the PLR means, basically, that a rejection is more likely to be a rejection of a false null than a rejection of a true null, thus the PLR means that a rejection is more likely to be correct than incorrect.

As an example, if β = .20, and α = . 05, the PLR equals 16. This means that a rejection is 16 times more likely to be correct (the null is false) than incorrect (the null is true).

The second property I focused on is the Negative Likelihood Ratio (NLR). The NLR is the ratio of the frequency of incorrect non-detections to the frequency of correct non-detections. In NHST-as-screening-test, the NLR equals the ratio of the probability of a type II error to the probability of a correct non-rejection: NLR = β / (1 – α). A small value of the NLR means, in essence, that a non-rejection is less likely to occur when the null-hypothesis is false than when it is true.

As an example, if β = .20, and α = . 05, the NLR equals .21. This means that a non-rejection is .21 times more likely (or 4.76 (= 1/.21) times less likely) to occur when the null-hypothesis is false, than when it is true.

The PLR and the NLR can be used to calculate the likelihood ratio of the alternative hypothesis to the null-hypothesis given that you have rejected or given that you have not-rejected, the posterior odds of the alternative to the null. All you need is the likelihood ratio of the alternative to the null before you have made a decision and you multiply this by the PLR after you have rejected, and by the NLR after you have not rejected.

Suppose that we repeatedly (a huge number of times) take a random sample from a population of null-hypotheses in which 60% of them are false and 40% true. If we furthermore assume that a false null means that the alternative must be true, so that the null and the alternative cannot both be false, the prior likelihood of the alternative to the null equals p(H1)/p(H0) = .60/.40 = 1.5. Thus, of all the randomly selected null-hypotheses, the proportion of them that are false is 1.5 times larger than the proportion of  null-hypotheses that are true. Let’s also repeatedly sample (a huge number of times) from the population of decisions. Setting β = .20, and α = . 05, the proportion of rejections equals p(H1)*(1 – β) + p(H0)*α = .60*.80 + .40*.05 = .50 and the proportion of non-rejections equals p(H1)*β + p(H0)*(1 – α) = .60*.20 + .40*.95 = .50. Thus, if we sample repeatedly from the population of decisions 50% of them are rejections and 50% of them are non-rejections.

First, we focus only on the rejections. So, the probability of a rejection is now taken to be 1.0.  The posterior odds of the alternative to the null, given that the probability of a rejection is 1.0, is the prior likelihood ratio multiplied by the PLR: 1.5 * 16 = 24. Thus, we have a huge number of rejections (50% of our huge number of randomly sampled decisions) and within this huge number of rejections the proportion of rejections of false nulls is 24 times larger than the proportion of rejections of true nulls. The proportion of rejections of false nulls equals the posterior odds / (1 + posterior odds) = 24 / 25 = .96. (Interpretation: If we repeatedly sample a null-hypothesis from our huge number of rejected null-hypotheses, 96% of those samples are false null-hypotheses).

Second, we focus only on the non-rejections. Thus, the probability of a non-rejection is now taken to be 1.0. The posterior odds of the alternative to the null, given that the probability of a non-rejection is 1.0, is the prior odds multiplied by the NLR: 1.5 * 0.21 = 0.32. In other words, we have a huge number of non-rejections (50% of our huge sample of randomly selected decisions) and the proportion of non-rejections of false nulls is 0.32 times as large as the proportion of non-rejections of true nulls. The proportion of non-rejections of false nulls equals 0.32 / ( 1 + 0.32) =  .24. (Interpretation: If we repeatedly sample a null-hypothesis from our huge number of non-rejected hypotheses, 24% of them are false nulls).

So, based on the assumptions we made, NHST seems like a pretty good screening test, although in this example NHST is much better at detecting false null-hypothesis than ruling out false alternative hypotheses. But how about the question of decisions as evidence for the reality of an effect? I will first write a little bit about the interpretation of probabilities, then I will show you that decisions are not evidence.

Sometimes, these results are formulated as follows. The probability that the alternative is true given a decision to reject is .96 and the probability that the alternative hypothesis is true given a decision to not-reject  is .24.  If you want to correctly interpret such a statement, you have to keep in mind what “probability” means in the context of this statement, otherwise it is very easy to misinterpret the statement’s meaning. That is why I included interpretations of these results that are consistent with the meaning of the term probability as it used in our example. (In conceptual terms, the limit of the relative frequency of an event (such as reject or not-reject) as the number of random samples (the number of decisions) goes to infinity).

A common (I believe) misinterpretation (given the sampling context described above) is that rejecting a null-hypothesis makes the alternative hypothesis likely to be true. This misinterpretation is easily translated to the incorrect conclusion that a significant test result (that leads to a rejection) makes the alternative hypothesis likely to be true. Or, in other words, that a significant result is some sort of evidence for  the alternative hypothesis (or against the null-hypothesis).

The mistake can be described as confusing the probability of a single result with the long term (frequentist) probabilities associated with the decision or estimation procedure. For example, the incorrect interpretation of the p-value as the probability of a type I error or the incorrect belief that an obtained 95% confidence interval contains the true value of a parameter with  probability .95.

A quasi-simple example may serve to make the mistake clear. Suppose I flip a fair coin, keep the result hidden from you, and let you guess whether the result is heads or tails (we assume that the coin will not land on it’s side). What is the probability that your guess is correct?

My guess is that you believe that the probability that your guess is correct is .50. And my guess is also that you will find it hard to believe that you are mistaken. Well, you are mistaken if we define probabilities as long term relative frequencies. Why? The result is either heads or tails. If the result is heads, the long term relative frequency of that result is heads. That is to say, the result is a constant and constants do not vary in the long run. Your guess is also a constant, if you guess heads, it will stay heads in the long run. So, if the result is heads, the probability that your guess (heads) is correct is 100%, however, if your guess is tails, the probability of you being correct is 0%. Likewise, if the result is tails, it will stay tails forever, and the probability that your guess is correct is 0% if your guess is heads and 100% if your guess is tails. So, the probability that your guess is correct is either 0 or 1.0, depending on the result of the coin flip, and not .50.

The probability of guessing correct is .50, however, if we repeatedly (a huge number of times) play our game and both the result of the coin flip and your guess are the result of random sampling. Let’s assume that of all the guesses you do 50% are heads and 50% are tails.  In the long run, then, there is a probability of .25 of the result being heads and your guess being heads and a probability of .25 of the result being tails and your guess being tails. The probability of a correct decision is therefore, .25 + .25 = .50

Thus, if  both the results and your guesses are the result of random sampling and we repeated the game a huge number of times, the probability that you are correct is .50. But if we play our game only once, the probability of you being correct is 0 or 1.0, depending on the result of the coin flip.

Let’s return to the world of hypotheses and decisions. If we play the decision game once, the probability that your decision is correct is 0 or 1.0, depending on whether the null-hypothesis in question is true (with probability 0 or 1.0) or false (with probability 0 or 1.0). Likewise, the probability that the null-hypothesis is true given that you have rejected is also 0 or 1.0, depending on whether the null-hypothesis in question is true or false. But if we play the decision game a huge number of times, the probability that a null-hypothesis is false, given that you have decided to reject is .96 (in the context of the situation described above).

In sum, from the frequentist perspective we can only assign probabilities 0 or 1.0 to a single hypothesis given we have a made single decision about it, and this probability depends on whether that single hypothesis is true or false.  For this reason, a significant result cannot be magically translated to the probability that the alternative hypothesis is true given that the test result is significant. That probability is 0 or 1.0 and there’s nothing that can change that.

The consequence of all this is as follows. If we define the evidence for or against our alternative hypothesis in terms of the likelihood ratio of the alternative to the null-hypothesis after obtaining the evidence, no decision can serve as evidence if our decision procedure is based on frequentist probabilities. Decisions are not evidence.

References 
Kline, R.B. (2013). Beyond significance testing. Statistics reform in the behavioral sciences. Second Edition. Washington: APA.

Posted on

Scientific with a small s

My inspiration for this blog’s motto comes from Zilliak & McCloskey (2004). They quote from Bob Solow’s Nobel Prize acceptance speech, after which they write:

“Solow recommends we “try very hard to be scientific with a small s”; but the authors we have surveyed in the AER [American Economic Review, GM], by contrast, are trying to be scientific with a small t.” (p. 544).

Their “small t” refers to the t statistic on the basis of which researchers determine the p-values they use to assess the statistical significance of their findings. A small p (smaller than .05) is usually taken to mean that the test result is statistically significant.

There are a lot of reasons to believe that null-hypothesis significance testing (NHST) is basically unscientific. That’s why I got convinced that you cannot do science with a small p (significance testing). I hope that after reading the blog posts yet to come, you will be convinced as well.  (If you can’t wait: Kline (2014) (see below) is a good place to start getting convinced).

What does it mean to be scientific with a small s? To Solow (as cited in Zilliak & McCloskey, 2004) it simply means thinking logically and respecting the facts.  To my mind, thinking logically as a prerequisite of being scientific (with a small s) includes thinking logically about the results of statistical analyses. For instance, that you should not mistakenly believe that a small p value means that it is unlikely that a result is due to chance, or that you should not mistakenly believe that the long term behavior of a decision procedure has anything to do with the evidence in your actual data (the facts).

Zilliak & McCloskey (2004) write about economic research, but significance testing is of course not limited to economic research. Kline (2013, p. 118-199) concludes in his chapter about cognitive distortions in significance testing (and he is putting it mildly):

“Significance testing has been like a collective Rorschach inkblot test for the behavioral sciences: What we see in it has more to do with wish fulfillment than reality. This magical thinking has impeded the development of psychology and other disciplines as cumulative sciences. […] the gap between what is required for significance tests to be accurate and characteristics of real world studies is just too great.”

So, this blog is about being scientific with a small s, with a main focus on the logic and illogic of NHST, because you simply cannot do science with only a small p.

References
Kline, R.B. (2013). Beyond significance testing. Statistics reform in the behavioral sciences. Second Edition. Washington: APA.
Zilliak, S.T., & McCloskey, D.N. (2004). Size matters: the standard error of regressions in the American Economic Review, Journal of Socio-Economics, 33, 527-547.